「光時計の時空構造」
(The space-time structure of the Light Clock)
村山 章 (Murayama Akira) 2004年12月 執筆
<index>
(注:印刷時は、「ページ設定」で、左右の余白を縮めてページ幅を広げて下さい。)
1.はじめに
相対性理論の解説には、光時計を使った時間の遅れの説明というものがある。これは、アインシュタイン自身によって提出された重要な論法であり、その上、中学生レベルのごく簡単な数式処理で、相対性理論特有の時間の遅れ等が導き出せることもあって、入門書の始めの段階で、必ずと言っていいくらい高い頻度で出てくる。この説明は、大抵の場合、入門段階であるが故に、相対性理論の時空構造を知らない状態、同時刻の相対性等の重要なパラダイム転換を充分理解していない状態で、聞かされることになる。
光速不変の原理を説かれたすぐ後で、ピタゴラスの定理と簡単な数式処理の知識があれば、時間の遅れは計算式として導き出せてしまうのである。だが、思うに、この段階で、すっきり納得できてしまう人は少ないのではないだろうか。というか、私としては、むしろ、ここの段階で納得できてしまう人は、あまり信用したくない。本当に深い洞察力を持つ者もいるだろうから一概には言えないけれど、単に解ったつもりになっているだけではないかと勘ぐってしまいたくなる。
相対性理論を学ぶ上で、第一の、そして最大の関門は、「同時刻の相対性」、「時空連続体」という概念を受け容れることなのだと思う。逆にそれができてしまえば、後は、数学的な知識獲得の問題で、世界観の大変革というハードルはそれほどないのではないだろうか。あとは、時空連続体は歪んでいるという概念さえ掴めば、地道に論理を追いさえすれば入っていけると思う。(たぶん。但し、楽ではない。)
だが、「同時刻の相対性」、「時空連続体」という概念を知らないか、知ってても充分に咀嚼していない状態で、光時計による時間の遅れの説明などを通じて無理やり納得させられてしまったような状態の人は、ふつふつと妙な気持ち悪さを引きずっていくわけで、この光時計による説明こそが理論の根源だと思っている人は、そこから演繹されたあれやこれやの理論(その中には、当然「同時刻の相対性」や、「時空連続体」という概念も含む)に対してもすべてみな、なんか、納得いかんな、という気持ちを伴って見てしまうのである。
そして、そういう気持ちを持った人の中には、果敢にも「相対性理論は間違っていた」と、「新理論」を展開しだす人も出てきてしまったりする。ただ、その新理論は、相対論出現当初から繰返し現れてきた、誤解と誤謬と内部矛盾に満ち満ちたズタボロ理論ばかりなのだが。
彼らが、決まって引き合いに出して、つついてやまないのが、光時計における、斜めに進む光の問題である。そうなのだ、ここが、ひっかかっているみたいなのだ。
本稿では、この光時計における、斜めに進む光について、「同時刻の相対性」、「時空連続体」という概念の元で再度見直すということをしてみようと思う。そして、この問題をきっかけにして、相対性理論を理解するとはどういうことなのかについても、考察してみようと思う。
私は、相対性理論は、論理的に理解可能なものだと信じている。つまり、科学理論として完全に正しいと思っている。(もちろん、未知の適用限界を超えない範囲においてである。) その一方で、相対性理論が心情的納得に至るまでには、大きなハードルがあるという事実も認めるべきだと思っている。これはこれとして、真摯に捉え、深く考えていくべき課題なのだ。だが、これは、哲学、ないし心理学の問題であって、物理学の問題ではない。心情的納得ができないことをもってして、物理理論としての相対性理論を否定してしまおうと、これ以上、ガラクタ理論を撒き散らすのは、人生の貴重な時間の無駄遣い以外の何ものでもない。そんな後ろ向きな態度はもうやめて前に進もうではないかと提言したいのだ。
が、その前に、とりあえず、相対性理論の基礎部分、妙な誤解は拭い去って、少なくとも論理的には理解しておこうではないか、ということで、起こしたのが、本稿である。
indexへ
(2)光時計に基づく時間の遅れの説明
2.光時計を使った時間の遅れと距離の収縮の導出
(1)マイケルソン・モーレーの実験
多くの相対性理論の入門書では、先ず、光を伝える媒体として想定されていたエーテルというものに対する地球の速度を測定しようとして失敗した、マイケルソン・モーレーの実験について、或いは、電磁気学の法則は光速が不変であることを強く要請しているといった事情などが解説され、ローレンツやポアンカレらの苦し紛れの理論的努力に対して、アインシュタインは光速は不変ということを原理として位置付け、そこから力学体系、時間・空間の概念そのものを変革していく道を選んだことが解説される。
光速という速さなるものが、一定不変というのは、従来の常識からすると、大変理解に苦しむ事である。例えば、秒速30万kmの光を光の半分の速さ(秒速15万km)で追えば、その光は元の半分の速さ(秒速15万km)になるはずというのが、常識であった。しかし、この原理は、光を光の半分の速さで追う者からしても、その光はやはり元の光の速さ(秒速30万km)なのだと言っているのである。常識では納得のいかないこの原理を先ず認めなさい、というところから、アインシュタインは展開していった。そして力学体系を大変革した。その中で速度の合成則も単純な加減算に基づくものではない新たな形式に書き直すことで、従来の常識的観念との矛盾も解決した。非常識な原理から、非常識と常識の双方を裏付けたわけである。
アインシュタインは、理論を展開していくにあたって、まず、「光速の不変性」を根拠に、時間を光で測る時計を定義した。これが光時計である。どういうものかと言うと、ある距離Lを隔てて鏡が置かれていて、そこに向って光を放ち、放ってから、反射して戻って来るまでの時間を単位時間と定義する。例えば、Lが15万kmなら、光の往復(30万kmの走行)にかかる時間をもって、それが1秒と定義するのである。
そして、この光時計は、どんな速度にいる者でも、つまりすべての慣性座標系で、通用するはずだと考える。なぜなら、光速は不変なのだから。
もし、光を伝える媒体エーテルというものがあって、光はそこを伝わるという観念のもとであれば、この光時計は、そのエーテルに対して静止している座標系以外使えないものである。エーテルに対して、移動している系では、往って戻って来るまでの時間は少し長くなる。それも光を放つ方角によって値が異なるはずである。マイケルソン・モーレーの実験では、エーテルに対する系の移動方向に対し平行方向に光が往復する時間と垂直方向に往復するする時間とで理論上差がある(※2-1)ことに着目して、地球のエーテルに対する移動速度を計ろうとするものであった。地球は自転しながら太陽の周りを秒速30kmで公転しているのだから、時刻や季節の違いで、エーテルに対する速度が異なるはずだと考えられた。当時としても充分な精度の計測であったにもかかわらず、この2方向での測定差は零であった。つまり、地球のエーテルに対する移動速度は常に零であった。(今日まで、さらに高い精度での計測が幾度も繰返されてきているが結果は同じである。)これは、宇宙にただ一つのエーテルが地球表面にぴったりくっついて地球の自転・公転に合わせて移動しているとでも考えない限り説明できないことである。そんな途方もない地球中心説はとても考えられないことだし、仮にもしそうだとしたら、幾多の天文学的観測事実と矛盾してしまうことになる。
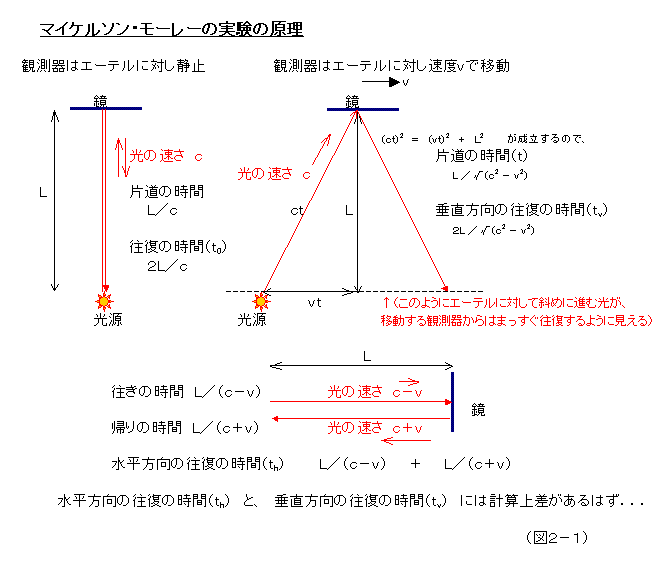
(※2-1)具体的には、
エーテルに静止した系での光の往復時間 t0 は、
t0 = 2L/c
(時間は、光の移動距離÷光の速度で求められる。)
エーテルに対して速さvで移動する系の移動方向に平行な方向での往復時間 th は、
th = L /(c - v) + L /(c + v)
= 2L (c/c2-v2)
= (2L/c)(1/1-(v/c)2)
(往きと帰りで、光の伝達速度が異なるから。)
エーテルに対して速さvで移動する系の移動方向に垂直な方向での往復時間 tv は、
tv = 2L / √(c2 - v2)
= (2L/c)(1/√(1-(v/c)2))
(片道の時間を t (= tv /2) とすると、
光はエーテルに対して斜めに進行していると考えられるので(図2-1)、三平方の定理より、
(ct)2 = (vt)2 + L2
これを解くと、
t = L / √(c2 - v2)
)
th と tv とでは、th の方がわずかに長い。
(vが零だと差はない。vが地球の公転速度と考えるなら、数ナノ秒の差。)
(なお、実際のマイケルソン・モーレーの実験では、光の往復時間をそれぞれの方向で実測したわけではなく、ハーフミラーを使って、2つの光線を重ね合わせ、到達時刻に差があれば、位相がずれて干渉縞が生じるはずだから、それを検出しようとしたが、検出されなかった、ということである。百年後の今日では、高精度の原子時計などがあるから、直接、到達時刻を計って確かめることも可能だ。もちろん、差は認められていない。これは、その時その時の技術水準に応じて、幾度も確認され追認されてきた事実である。)
アインシュタインは、このマイケルソン・モーレーの実験結果とは独立に、電磁気学上の洞察から、そもそも光の媒体エーテルという仮説上の存在を疑問視していた。光量子のアイデアも影響していたかもしれない。光は、エーテルなる固定的媒体を伝わる波のようなものとして考えるべきではない。そして、彼は、真空での光速を宇宙の法則、基本定数と考えた。(以下、特に断らない限り、ここで言う「光速」とは、「真空での光速」のことである。蛇足かもしれないけれど、幼稚な誤解が後を絶たないようなので念のため。)
そう考えることで、先程の光時計は全ての慣性座標系で、全く平等に機能する。
そして、ここが、重要なことなのだが、この光時計で、単位距離、ないし単位時間を定義してしまおうと考えた。つまり、どんな慣性座標系でも、光速が一定値になるように、単位距離と単位時間の関係は成り立っているべきだと考えた。そのためには、単位距離、単位時間が異なる座標系間で互いに一致している必要はないと考えた。ただし、特権的な慣性座標系があってはならない。すべての慣性座標系は互いに対等であるというこのガリレイ以来の大原則は崩してはならない。これには、すべての方向は対等であるということも含意されている。そういう前提で特殊相対性理論は組み上げられていった。
ここにおいて、すでに大いなるパラダイム変換がなされているわけなのだが、多くの人はまだこの時点では、それに気づかない。気づかないまま、昔ながらの常識的な時間や空間についての観念を引きずったまま、この先の論理展開を追って行くことになる。
アインシュタインは、運動する方向の単位距離と単位時間は、座標系ごとに異なっている可能性があると考えた。しかし、運動する方向に垂直な方向では、座標系間の相対速度の影響は受けないと考えられる。そちら方向の速度成分は零なのだから。それで、運動方向に垂直な方向に向かって光を放ち、その先の鏡に反射して戻ってくる光時計を想定することにした。互いに移動している座標系それぞれで、この向きの光時計を持つ。光源から鏡までの距離は、どちらの座標系でも等しいとする。垂直方向の距離によって、座標系間で共通できる距離単位が提供できたのである。いわば、これから時間空間の単位を光速に基づいて定義していくための最初の距離単位の種を取得したわけだ。それで、この共通の距離単位を定数である光速で割れば、共通の時間値が得られるわけで、これを(この共通の距離単位に対応した)時間単位と考えるのである。
ここまでは、それぞれの座標系で、その座標系に対し静止している光時計について考えたことである。今度は、相手の座標系の光時計、つまり運動している光時計について考える。
この光時計の光源から出た光は斜めに進む。(斜めに進まないとかと主張して本まで出してがんばっている方もおられるみたいだが、斜めに進む光でなければ、運動座標系の鏡に当たって反射しないから、光時計の役割を果たさない。レーザーを使った場合はと言えば、移動するレーザー発射装置では、斜め方向に光は整えられるから、斜めにレーザー光は進む。)斜めに進んだ光は、移動する鏡に反射して斜めに跳ね返って、移動する光源にぶつかる。これを、この光時計といっしょに移動している人は、光は静止した鏡にまっすぐ向かって行き、まっすぐに反射してもとの光源の位置に戻ってきたと観測するわけだが。
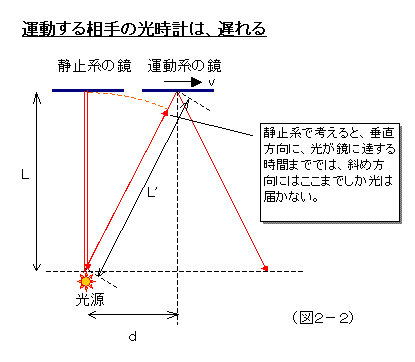
さて、斜め方向だが、これは当然、垂直方向よりも長い距離である。しかし、光はあらゆる方向に、一定の速さで動く。(それが原理だ。)すると、垂直方向へ光が静止系の鏡に届く時間では、斜め方向の光は、運動系の鏡の場所には到達できないことになる。鏡に届くまでの時間が、仮に0.5秒だとすると、運動系の光時計は、0.5秒よりも少し前を指しているということになる。運動系にとっては、斜め方向に行く光が鏡に到達した時点こそが0.5秒だと考えられるのだから。つまり、静止系から判断すると、運動する光時計は、静止系の光時計の0.5秒の時点で、0.5秒を指す状態に達していない、つまり、遅れているということになる。
それで、具体的にどれだけ遅れていることになるかというわけだが、
t は静止系の鏡までの到達時間、
t' は運動系の鏡までの到達時間とする。
仮定により、光速cは、どちらでも同じとする。すると、
運動系の鏡までの光の移動距離 (直角三角形の斜辺)
L' = c t' ・・・(1)
静止系の鏡までの光の移動距離 (直角三角形の高さ)
L = c t ・・・(2)
運動系の静止系に対する移動距離 (直角三角形の底辺)
d = v t' ・・・(3)
なので、三平方の定理より、
L' 2 = L 2 + d 2 ・・・(4)
が成り立ち、これに、先の(1)、(2)、(3)式を代入して、計算すると、
c2 t'2 = c2 t 2 + v2 t' 2
(c2 - v2) t' 2 = c2 t 2
t'2 = ( 1/(1 - (v/c)2)) t 2
正の根を取って、
t' = ( 1/√(1 - (v/c)2)) t
行きも帰りも同じと考えられるから、往復時間は、2倍となり、
(2t') = ( 1/√(1 - (v/c)2)) (2t)
ここで、
γ = 1/√(1 - (v/c)2)
としよう。すると、
(2t') = γ (2t)
γ ≧ 1 が常に成り立つから、 (2t') ≧ (2t)
つまり、運動系での光の往復時間は、静止系での光の往復時間の γ 倍に遅れていることになる。
具体的にvが光速の60%(秒速18万km)の場合だと、(v/c)は0.6で、γ の値は、1.25になる。1.25倍に運動する相手の光時計は遅れるわけだ。
さて、以上の議論は、裏返して、先程、運動系としていた座標系を静止系とみなし、静止系とみなしていた座標系を反対方向に移動する運動系とみなして考えた場合も、同様に成立する。つまり、A系、B系二つの座標系のどちらか一方が、絶対的な意味で一方的に光時計の進みが遅れるということではなく、互いに同等に、相手側の光時計が自分側から判断すると、遅れていると言い合う関係なのである。
(※別様の解説、「運動する相手の光時計の遅れ」も参考にして下さい)
相対性理論では、さらに、相手の座標系の距離が縮むことも重要な論理的帰結である。これは、フィッツジェラルド・ローレンツ収縮と呼ばれている。実は、アインシュタインに先駆けて、フィッツジェラルドやローレンツが、あらゆる物体はエーテルの中を進行すると縮むという仮説を立てて、先のマイケルソン・モーレーの実験結果を説明したり、電磁気学を基礎付けようとしたりという試みがなされており、それに敬意を表して名づけられている。従って、このアイデアはアインシュタインオリジナルのものではないのだが、彼は、光速不変の原理からこれを基礎付けたのである。
では、なぜ、光速が不変だと、運動する相手の座標系の距離が収縮すると考えねばならないかについて説明しよう。
アインシュタインは、距離単位というものについても、光速を使って定義した。光は、秒速約30万km(299,792.458 km/sec)で伝わる。これは、すべての慣性座標系に共通した値である。ということは、光が単位時間に進む距離が、単位距離であると定義してしまえば、この距離単位の定義は、すべての慣性座標系に共通して通用するはずのものだと考えた。時間単位を1秒に取れば、この時間で光が到達する距離、仮に1光秒と名づけると、それが距離の基本単位となる。これはメートル系に換算すれば、約30万km(299,792.458 km)である。
さて、それで、互いに移動する関係にある座標系間で、距離単位はどうなるかが問題である。従来の常識では、距離の単位は、すべての座標系で共通であった。しかしそう言えなくなってしまったのである。
ここでも、座標系間の相対速度vは光速の60%(秒速18万km)の場合で考えよう。
この場合、 (v/c)=0.6 なので、γ の値は 1.25 である。(図2-3)
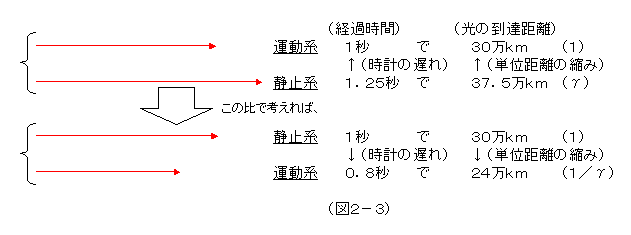
定義により、運動系での1秒間の光の到達距離、それが運動系での1光秒(=30万km)である。ところで、運動系の時計は、先程の考察によれば、静止系からすれば遅れているわけだから、このとき静止系ではすでに 1.25秒経ってしまっているはずだ。すると、光はこの時間で静止系では、1.25光秒(=37.5万km)の距離まで進める。
この比で考えると、静止系の1秒間での光の到達距離(1光秒(=30万km))は、運動系では 1/1.25(=0.8)秒間の光の到達距離(0.8光秒(=約24万km))であるはずだ。
運動する相手の単位距離、すなわちモノサシは縮んでいる。一般に、その度合いは、時間の遅れの度合いの逆数と考えればよいから、
1/γ = √(1 - (v/c)2) ( ≦ 1)
である。これから分かるように、二つの系の相対速度 v が光速に比べて充分に小さければ、ほとんど1、すなわち両系の尺度に違いはほとんどないのだが、光速と比較しうるくらいに大きくなっていけば、1より小さな値になっていく、すなわち運動系の尺度の縮み具合は大きくなっていく。
以上の議論も、やはり裏返して、先程、運動系としていた座標系を静止系とみなし、静止系とみなしていた座標系を反対方向に移動する運動系とみなして考えた場合も、同様に成立する。つまり、A系、B系二つの座標系のどちらか一方が、絶対的な意味で一方的に距離単位が縮むということではなく、互いに同等に、相手側の距離単位が自分側から判断すると、縮んでいると言い合う関係なのである。
(4)光速と時間・空間の計量単位
ところで、光の速さは、物理の基本法則、宇宙の基本定数だ、ということなのであるから、これに基づいた光時計は、すべての時計の基準になりうるものである。こう言うと、天下り的な強弁に聞こえるが、実際、光速は、電磁気学の法則から導出されるものであり、電磁気力は、重力を除けば、人類が感じるほとんど全ての力の根源であるわけで、光時計だけが、他の時計と独立して遅れるということは、考えられないことである。だから、光時計の示す時間との比で、すべての物理現象の経過時間は表現可能なはずと考えて差し支えない。そして同様に、光速に基づいて定義された距離単位も、すべての距離単位の基準たりうると考えることが可能である。
とすると、相手の座標系に乗ったすべての時計、いわば、時間そのものが互いに遅れていると考えねばならないことになり、同様に、相手のあらゆる物体の長さ、いわば空間そのものが互いに縮んでいると考えねばならないことになる。心理的な時間とか、歩幅による距離とかといった曖昧な時間や空間の尺度も、その曖昧さは伴いつつも、その平均的なスケール、規模は、やはり遅れたり縮んだりしているのだと考えねばならない。
光速に基づいて時間・空間の計量単位を基礎づけるというアイデアは、単に光速不変の原理を原理として定立したからという論理学的観点からのみ理解しては充分ではない。このアイデアの根底には、光、即ち電磁波というものの宇宙における普遍性という前提があることを理解すべきだ。電磁気は、原子や分子の間で働く力の基礎でもあることが当時はっきりしてきたという背景がそこにはあるだろう。そして、真空での電磁波の速さ、即ち光速は、電磁気学の基本方程式から導出されてしまう値なのである。すべての慣性系で物理法則は普遍的に成立するはずだというガリレイ以来の信念をアインシュタインはただひたすら電磁気学まで含めて貫徹させたかった。それが光速不変の原理なのである。
そして、実際にこの理論が導く結果に基づいて、様々な観測事実と照らし合わせると整合的にすべてつじつまが合ったのである。例えば、磁気力が、ローレンツ収縮で説明できたりしたわけだ。だが、現在はいたるところで、光速の不変性は直接実証されていて、もはや論理的つじつま合わせのための仮説だなどと考えるにはあまりにも無理がありすぎる。光速の99.999999%以上に加速された粒子から発せられた光(光子)はどの方向にもやはり光速でしかないことは、高エネルギー研究所では日常的な観測事実なのだ。もし光速不変が間違っていて従来の速度の加法則が成立するなら、光速のほぼ二倍の光とか殆ど止まっている光とかが観測されるはずだが、そんな観測事実は全くない。そして、光速の絶対性は、何も電磁気の普遍性に依拠するに留まらない、遥かに大きな普遍性である。それは、相対性理論発表当時ではまだアインシュタインの信念上のことでしかなかったかもしれないが、このことは、電子や陽子に限らずあらゆる素粒子の振る舞いが相対性理論に従った結果を示していることから、現在では、信念、要請、仮説の面影が完全に払拭された実証事実になっている。いまや、光速は全ての速度の基準であり、時間や距離の基準定義の根拠たりうる普遍的定数であると、充分な実証根拠に基づいて言えるのである。
以上が、光時計を使った時間の遅れ、並びに距離の収縮の説明である。
ここで、これまでの論理展開をもう一度振り返ってまとめてみよう。
[1] 慣性座標系が互いに同等という(特殊)相対性原理と、光速不変の原理の定立。
↓
[2] 光を鏡に反射させて戻るまでの時間を単位時間とする光時計の定義
↓
[3] 座標系間の移動方向に垂直な方向での距離は互いに不変と想定。
(ここで距離単位の種を取得)
↓
[4] 移動方向に垂直な方向に往復させる光時計を使って考察。
光速不変なら、運動する側の光時計は遅れていると考えざるをえない。
(どれだけ遅れているか定量的に算出可能。三平方の定理によって導出。)
↓
[5] 距離単位を光の単位時間での到達距離によって定義
↓
[6] 運動する側の光時計は遅れているのなら、運動する側の距離単位は縮んでいると考えざるをえない。
(どれだけ縮んでいるか定量的に算出可能。時間の遅れ率の逆数。)
↓
[7] 以上は、逆に、運動系としていた座標系を静止系とみなし、静止系とみなしていた座標系を反対方向に移動する運動系とみなして考えた場合も、同様に成立する。両座標系は、互いに相手の時計が遅れ、距離単位が縮んでいると判断し合う関係にある。
以上である。こうまとめると、至極シンプルな論理だ。
だが、この説明を聞いただけでは、論理的には、一応理解できたとしても、心情的には、なんかしっくりこないという人が多いのではないだろうか。
Aからすれば、Bの時計は遅れている(物差しは縮んでいる)、とすれば、逆にBからすればAの時計は進んでいる(物差しは伸びている)というのが、我々の慣れ親しんだ常識である。なのに、BからするとやはりAの時計の方が遅れている(物差しは縮んでいる)というのである。光速不変という非常識を呑んだのだから、こういう非常識も呑んでしかり、と素直に受け容れることができてしまう人もいるかもしれないけれど、なんか、どこかで騙されているような気になってしまう人が多いのではないだろうか。
これは、心の中で重要なパラダイム転換ができていないからなのだ。実は、この時計の遅れが語られる前か後か(通常は前)に必ず語られることとして、「同時刻の相対性」ということがある。これも光時計を使って説明されることが多い。次にこれについて説明しよう。
indexへ
3.同時刻の相対性と時空概念
光時計は、相対性理論では、前節で述べたように基本の時計として扱われ、離れた場所での時刻合わせにも使われることになっている。また、遠く離れた場所での出来事の同時性の定義にも利用される。離れた場所に置かれた鏡に向かって光を放ち、放った時刻と、反射して戻って来た時刻の中間の時刻が、かなたの鏡でその光が反射した時刻と同時刻だと定義するのである。往きも帰りも同じ速さなのだから。

これだけ、聞くと、なんか当たり前のことを言っているだけのように思われるかもしれない。静止した状態で考えれば、そうだ。だが、光を放った時点で、放った所から、鏡の方向に向かって走って行く者の立場で考えると妙なことが結論される。彼は、鏡で反射した光を静止している者より早く受け取る。彼は、反射した時刻をいつと考えるか、というと、彼にとっても、やはり光は往きも帰りも同じ速さなわけだから、光が放たれた時刻と、反射して戻って来た時刻の中間の時刻が、反射した時刻と同時刻だと考える。だが、この時刻は、静止している者が判断した反射した時刻よりも前の時刻である。つまり、ある事象(この場合、光の反射)について、それと同時刻である事象は、座標系によって異なるのである。(図3-1)
こんな変なことになるのは、光速が不変だからだ。常識では、鏡に向かって走る者にとって、鏡に向かって放たれた光の速さは自分の速さ分遅く、反射して戻ってくる光は自分の速さ分速くなるわけで、従って、反射する時刻は、中間時刻ではなく、それより後だと判断される。(つまり、往きは長くかかって鏡にたどり着き、帰りは短い時間で戻る。)
「同時刻の相対性」という非常識は、このように、「光速不変」という非常識と直結したものである。つまり、相対性理論を理解するには、この「同時刻の相対性」を認めるという時間概念に対するとてつもないパラダイム転換をしなければならないのだ。そしてここが本質的に重要なのだ。
アインシュタインは、同時刻の相対性を一般向けに説明するのに、列車の話を使った。走行する列車のちょうど中央に光源を置いて、列車の前方と後方に向けて同時に光を放つ。光速は、等しいから、この列車に乗っている者にとっては、光は前端、後端同時に到着する。ところが、列車の外でこれらの光を見る者からすると、やはり前方への光の速さと後方への光の速さは等しいわけで、すると、列車の後端は、光に向かって行くから、先に光が到着し、前端は、光から逃げる方向に走るから、遅れて光が到着する。前端への到着、後端への到着という二つの事象(出来事)は、走行する列車に乗る者にとっては同時刻であり、列車の外で止まっている者にとっては、同時刻ではないという事態が生じるのである。(図3-2)
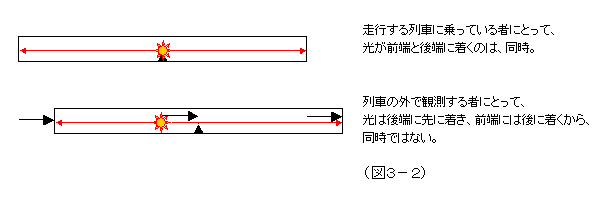
常識の世界では、例えば、静止したエーテルの中を列車が走り抜けていると仮定した場合、列車から見た光の速さは前方に向かうものは遅く、後方に向かうものは速くなるはずである。それで、立場によって、二つの出来事が同時であったりなかったりなんてことはありえないことになっている。光速が不変だと認めるということは、何よりもまず、この「同時刻の相対性」を認めることと不可分なのである。
ところで、列車の前端、後端から、列車にとって、同時刻に光が発せられたとすると、当然、列車の中央には、同時に光が届く。これは、列車の外の観測者にとっては同時でないかといったら、そんなことはない。距離を隔てていない同じ場所での同時刻の出来事は、どんな座標系からでも同時刻だ。もし、同時に光が中央に届いたら爆発するような装置を中央に置いておけば、列車に乗っている人にとっても、乗ってない人にとってもそれは爆発する。それでは同時刻の相対性はどうなったのか、と言えば、この場合、列車の外の観測者にとっては、光が発せられた時刻が同時ではないのだ。外の者にとっては、後端からの光が先に発せられ、前端からの光は後から発せられ、結果として列車の中央で両方の光ははちあわせしたことになる。距離を隔てた事象である、列車の後端と前端からの光の発射は、座標系によって同時であったり、なかったりするのである。これも蛇足かと思いつつ、いまだにこれを理解できない人がいるみたいなので、念のため。(図3-3)
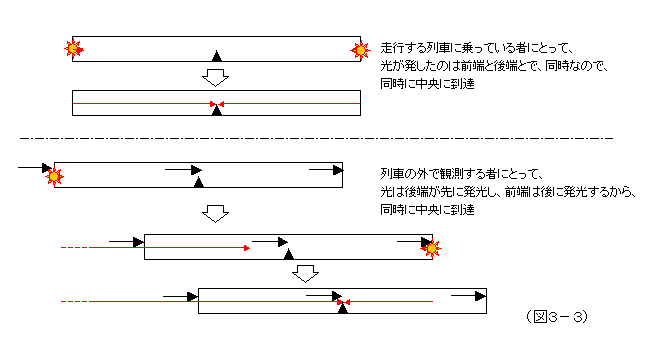
しかし、ここまで一応、論理的に理解したとしても、「また、奇妙な結論がひとつ追加されたのか、それにしたって、同じ二つの出来事が同時であったりなかったりするなんて、どういうことだ、さっぱりわけわからん」という気持ちに満ち満ちている人は、やはり多いのじゃないだろうか。光速不変はもはや否定しがたい観測事実である以上、そこからの論理的帰結なのだから、受け容れるしかないのだときっぱりここで割り切れる人は、脱落することなく、前に進んで行けるだろうけれど、なんか、さらにわけが解らなくなってしまう人も少なくない。
とにかく、光時計に基づく相対性理論の解説は、多くの人に対して、論理的だが、煙に巻かれたような、きつねにつままれたような、腑に落ちない感情をどこかに残すのだ。
だが、論理的推論は容赦なく進行していく。数学的には、異なる座標系間の一般的な座標変換則はどうあるべきか、ということで、これまでの考察をもとに、あるいは、一般的な一次変換に、光速不変、変換の相互対称性などの条件を加味して係数を定めるなどののやり方で、ローレンツ変換式が導き出される。求め方は色々あると思う。例えば、異なる系での球面波の方程式(光速不変のためどちらの系でも同じ形式)に、一般的な一次変換式を代入して得られる、変換式の係数間の関係式から係数値を求めるというアインシュタインが示したやり方が、よく紹介される。ここで、一次変換(比例的な関係間の変換)が前提されるのは、方程式の形状から、2次以上の項はありえないという判断が成り立つからでもあるが、これは、慣性系同士の関係の、場所や時間の変化に対して比例的な対応関係が成立するという性格を反映しているとも言える。いずれにせよ、この変換式さえ、手に入れれば、これまで説明してきた、時計の遅れ、距離の収縮、同時刻の相対性は、計算式を解く形で導き出せる。さらに、相対論的な速度の加法則、相対論的力学、電磁気学の相対論的基礎付けなど、特殊相対性理論のあらゆることが計算で導出できる。これは強力な汎用ツールである。だが、本稿では、ビジュアルな解説を中心に置きたいので、ローレンツ変換式から計算を使って、これらを導出するやり方の説明はあえて割愛しよう。相対性理論の解説書にいくらでも書いてある。一応、式自体は以下に、掲げておこう。
(ct,x)系 → (ct’,x’)系 へのローレンツ変換
ct’ = γ (ct - (v/c) x)
x’ = γ ( x - (v/c)ct)
(ct’,x’)系 → (ct,x)系 へのローレンツ変換
ct = γ (ct’+ (v/c) x’)
x = γ ( x’+ (v/c)ct’)
ただし、
γ = 1 / √(1-(v/c)2)
(ここで、時間座標を t ではなく、ct としたのは、時間の単位を、光速が1となるような単位系にして表現したかったからである。そうすると、空間と時間がきれいに対称的に表現できる。)
式から見て、従来のガリレイ変換と比べて、注目すべき特徴を簡単にのべておこう。そもそも、ガリレイ変換では、時間座標はすべての座標系で共通だから、あえて、t’= t なんて式は掲げることもしなかった。x’ = x - vt という、「時間とともに速さ×時間分、位置がずれる」ということを述べるだけのものであった。これに比べてローレンツ変換では、第一に、時間座標の変換に計算が必要ととなり、そこに空間座標の項が入っている。これは、距離を隔てれば同時刻が座標系に依存して相対的になってしまうことを端的に示している部分だ。次に、γ 倍されていること、これが、互いに相手の時計が遅れることに対応している。距離の収縮とも関連している。
計算できれば、それは理解できたことと、素直に受け容れられる人は、もう悩まない。割り切って前進するばかりだ。だが、計算できる、つまり論理形式に従って理解できることと、心情的に納得できることとのギャップに違和感を覚え、その違いに重大性を感じ、そこにこだわり続ける人は、いらいらしてくるだろう。もしこれが、純粋に数学上でのことなら、あるいは、自分の日常とはるかにかけ離れた世界のことなら、こういう心情は、起こりにくいかもしれない。だが、ここで対象にしているのは、いつも身近に生活の中に基底的に存在している時間と空間なのだ。いくら速度の規模が日常体験する規模と違うからと言われても、容易には受け容れがたい内容なのである。
さて、ここらあたりで、時間と空間を統合させた時空図が登場する。完全な形では、3次元の空間+1次元の時間で4次元なのだが、これは描けないどころか、イメージすらできないのだから、通常、説明のためには、空間を1次元か2次元に縮めて、余った空間次元を、1次元の時間を表現するのに割り当てる。運動する点は、時空図の中では過去から未来の方向へ向かう線で表現される。これを「世界線」と呼ぶ。2次元の平面図形の運動は、3次元の棒状の立体である。3次元の立体の運動は4次元超立体になるので、数学的形式でしか表現できない。イメージするのは無理である。
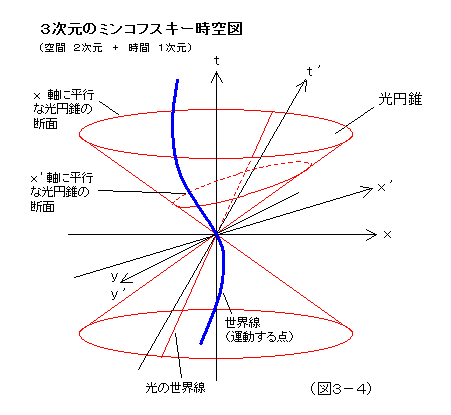
ここでは、ある点の運動は、ある世界線が、基準世界線(座標系の時間軸)に対してどう傾くかで表現される。光の1点(光子、ないしある光の位相部分)の運動もある傾きを持った世界線で表現される。「光速不変の原理」とは、ある方向について、この傾きが、一定だということで表現される。ある原点から発せられうる光の世界線は空間を2次元で考えた場合だと、360度あらゆる方向に行きうるから、すべてを合わせると、頂点を付き合わせたような2つの円錐面で表現される。これを「光円錐」と呼ぶ。いかなる世界線も、この光円錐の傾きを超えて傾く(速度を増す)ことはできない。その意味で、これは光速という速度の壁を表現している。実際の4次元で、この光円錐がどんな形をしているかは、思い描けない。光円錐のある瞬間の断面は円や楕円になるが、4次元時空内の光円錐は、「断面」が球面や回転楕円体面になるような、何かとしか言いようがない。
この時空図は、アインシュタインの大学時代の教師でもあった、数学者ミンコフスキーが考案したので、「ミンコフスキー時空」と呼ばれる。このアイデアが提案されるまでは、「時空」と言う観点から相対性理論が語られることはなかったし、アインシュタイン自身も最初は抵抗感があったらしい。しかし、一般相対性理論に向かう過程で、アインシュタインはこのアイデアを完全に自分のものにしたばかりか、それを超えて歪んだ時空という観点でより普遍的な幾何学体系を使うところまで突き進んだ。
旧来からあるオーソドックスな教科書では、相対性理論が語られる歴史的経緯を反映してか、このミンコフスキー時空は、特殊相対性理論のあれこれの解説がなされた後の方にやっと登場する例が多いように思う。しかし近年の教科書では、定評のあるシュッツの「相対論入門」が典型的にそうであるように、かなり、はじめの段階から、この時空図を登場させていく傾向が強い。及ばずながら、当サイトで掲載している拙稿「相対性理論と同時刻の相対性」でも、まず、時空図から入って相対論を説明する方式を取らせてもらった。もちろん、その意義を自覚してのことである。先程まで展開してきた、光時計を使った解説というのは、ある意味、古典的な解説方式とも言えるのかなと私は思っている。
この時空図を使うと、「同時刻の相対性」、「時計の遅れ」、「距離の収縮」などは、ビジュアルに、かつ、統一的に理解ができるようになる。
(2-1)時空的観点からの「同時刻の相対性」
まず、「同時刻の相対性」についてだが、これは端的だ。ミンコフスキー時空では、一般に、時間軸が傾けば、空間軸も傾く。空間軸というのは、その座標系にとってのある時刻を表す線であり、その線上の点は全て同時刻である。それの傾きが座標系によって違うのだ。これは、ローレンツ変換で、時間座標の変換に空間座標の項が入っていることに対応している。
時空図というのは、なにも相対性理論のミンコフスキー時空が最初のものではない。物の動きを時間軸と空間軸の交差する座標上で表現することはよくなされてきたことである。身近な例では、鉄道のダイヤグラムがそうだ。縦軸に時刻、横軸に路線上の位置を表現して、それぞれの列車が何時にどの駅に到着し発車するかをプロットして線で結ぶ。これはまさに世界線の例である。時空図は、元来それほど馴染みの薄いものではない。ただ、相対性理論以前において、同時刻を表す横軸、すなわち空間軸が水平でなくなる、傾くということはなかった。そんなことは、考えだにしなかったことである。それが傾くのである。
何故、傾くか、と言えば、傾くからこそ、「光速不変」が保証されるのである。光速が不変、とは、ある光の世界線の時間成分と空間成分の比が、どんな座標系で表現しても一定であるということである。そのためには、時間軸が傾いた座標系では、それと対称的な形で、空間軸も時間方向に傾かないことには、成立不可能なのだ。
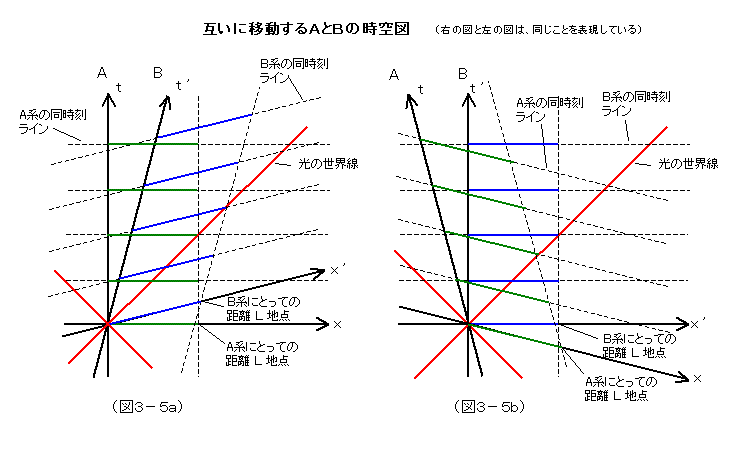
上の図は、互いに移動する関係にあるA系とB系を空間次元を1次元にして表現したものである。この図は、同じ長さLの列車とか細長い宇宙船とかがすれ違うさまを描いていると考えてもらってよい。緑、ないし青の実線の線分が、それぞれの座標系における、ある時刻の列車ないし宇宙船である。
図3-5aで、B系では、空間軸、すなわち同時刻の時空点の集合は傾いている。それゆえ、光が進む過程でどれだけの時間で、どれだけの距離に到達するかの比が、直交系であるA系と同じ値にに保てる。空間軸の傾きこそは、光速不変を根底で支えていることなのである。
ところで、運動は相対的なので、ある座標系だけが、特権的に直交系になるのはおかしい。A系はB系に対して、左方向に移動しているとも考えられる。B系を基準にして、これを直交系として全く同じ状況を描けば、A系の時間軸は左に傾くわけだが、今度は、A系の空間軸が、下に傾く。これも光速不変を保つ形で傾くのである。実は、直交系か斜交系かは、本質的な事柄ではない。互いに運動しているどちらを直交系に選んでもいいし、双方を斜交系にしてしまってもいい。単なる表現上の違いでしかない。ただ、言えることは、直交系、すなわちデカルト座標系で表現された方が、計算上の扱いが簡単になるということである。特殊相対性理論では、慣性座標系、即ち、直線的な座標系が基準として扱われるから、必ず、どちらかを直交系にできる。即ち、図3-5aか、図3-5bのいずれかのパターンにできるから、計算のしやすい方を選べばよい。
それでは、先ほど、光が鏡に反射する過程を使って説明した「同時刻の相対性」を、時空図を使って再度説明しよう。
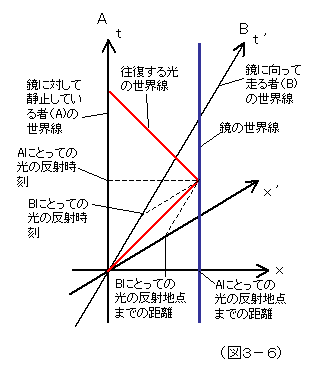
右の図3-6は、図3-1に対応した時空図である。A系は、静止する者、B系は、鏡に向かって走る者の座標系であり、光(の1点)が鏡に当たって反射して戻ってくる過程が、光の世界線として描かれている。見ての通り、B系の空間軸は、時間軸の傾きに対応して傾いている。
ここで、光が鏡に当たって反射した時刻が、問題である。A、Bどちらも光速は、往きも帰りも同じであるから、発光してから戻ってくるまでの時間の中間の時刻が、反射の時刻だと判断する。すると、双方で、その時刻にずれが生じることが、図から読み取れるであろう。
次に、列車の中央から前端、後端に向けて光を放った事例の時空図を描いてみよう。図3-7は、図3-2に対応した時空図である。左右のa図とb図との違いはどちらを直交系に選んだかの違いだけである。
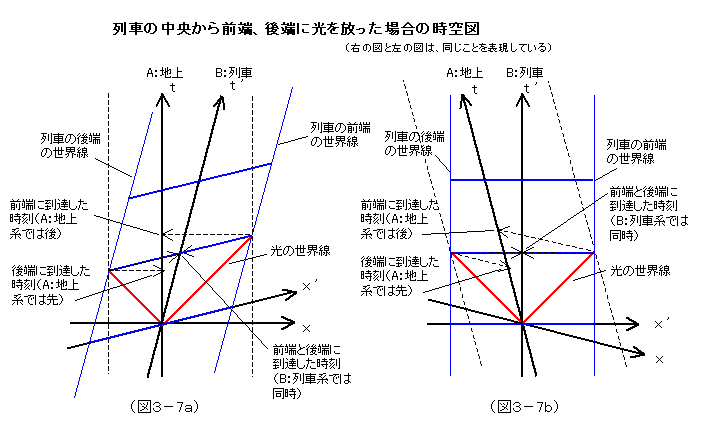
B:列車系では、前端、後端には、同時に光が到達することになる。しかし、A:地上系では、先に後端に光が到着し、その後、前端に光が到着する、という具合に、到着時刻は、同時刻ではないと判断されることになる。空間軸が傾くからそうなるのだということが、図から読み取れる。
さらに、列車の前端、後端から中央に向けて光を放って同時に中央に到達する事例の時空図を描いてみよう。図3-8は、図3-3に対応した時空図である。これも、左右のa図とb図との違いはどちらを直交系に選んだかの違いだけである。
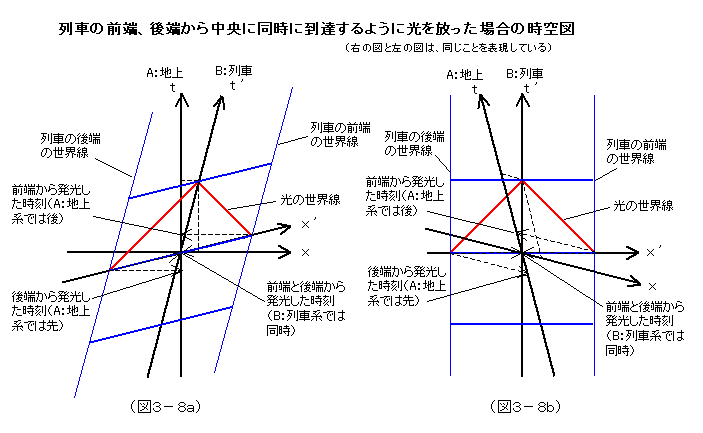
B:列車系では、前端、後端からは、同時に光が発光した故に、列車の中央で同時に、二つの光が到達したと判断される。しかし、A:地上系では、先に後端から光が発光し、その後、前端から光が発光したが故に、列車の中央で同時に、二つの光が到達したと判断される。このように距離を隔てた事象(ここでは発光)は、座標系によって、同時であったりなかったりするのである。これも、空間軸が傾くからそうなるのだということが、図から読み取れるはずだ。
(2-2)時空的観点からの「時計の遅れ」と「距離の収縮」
次に、「時計の遅れ」と「距離の収縮」について、「時空」という観点から、説明していこう。
ここでは、時間における「単位時間」、空間における「単位距離」というものについて考えねばならない。まず、相対性理論以前のガリレイ変換(ニュートン力学)が成り立つ世界の時空図を考えよう。
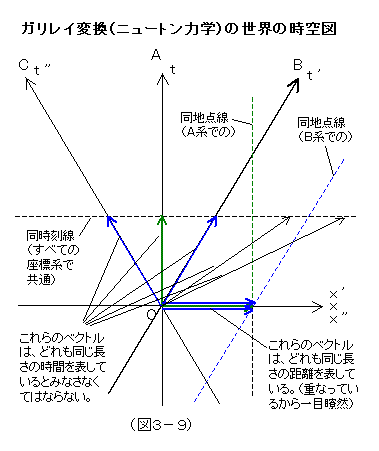
図3-9がそれである。時空図というのは、別に相対性理論特有のものではない。時間軸と空間軸を交差させたグラフ(ダイヤグラム)は、昔から考えられ、実用にも供せられてきたものである。ただ、相対性理論の時空図と決定的に違うのは、空間軸が傾くことがない、ということである。空間軸というのは、言い換えれば、ある時刻に等しい時空点を結んだ線、同時刻線である。これは、すべての座標系で共有しているものと相対論以前では考えられてきたわけだ。それゆえ、時間の進行は、どの座標系にとっても絶対的なテンポで進んでいく。
図3-9で、斜め上に向いた矢印(ベクトル)は、すべて、同じ時間の長さ(例えば単位時間)を表している。長さは、それぞれ違うではないか、直交系の単位時間ベクトル(緑色)が一番短く、速度の速い斜交系になるほど、矢印の長さは長くなるではないか、と思うかもしれないが、これは、「時空」を空間的に表現してしまっていて、ユークリッド空間の基準をそこに当てはめて見てしまうところからそう思えてしまうことであり、直交系をどれに割り当てるかは任意であることをかんがみて、この斜めになることからくる長さの伸びは、単なる表現上の事情から生じたものとして差っ引いて考えなくてはならない。(直交軸からの傾きをθとすれば、各ベクトル長をcosθ倍に縮めた補正値が正味の時間の長さに相当。「時空」というのは、ニュートン力学の前提においても、すでにユークリッド空間的ではないのである。) とにかく、ここで重要なことは、同時刻線の向きが、唯一絶対であるというこの時空図の特徴に留意しておくことである。そして、それゆえに、単位時間の長さは、どの座標系でも一定なのである。
一方、空間的な長さを表すベクトルは、空間の方向を(例えばx軸方向に)限定すれば、互いに傾き合うことはないから、同じ長さなら、ぴったり重なり合う。だから、座標系の違いで単位距離がどうこうなど、およそ考える余地はない。そして、ユークリッド空間内では、回転によって距離が変化することはない。よって距離単位が、どの座標系でも絶対不変なのは自明なのだ。
以上の旧来型時空図の特徴を念頭に置いた上で、次に、相対性理論における時空図を見てもらいたい。図3-10がそれである。
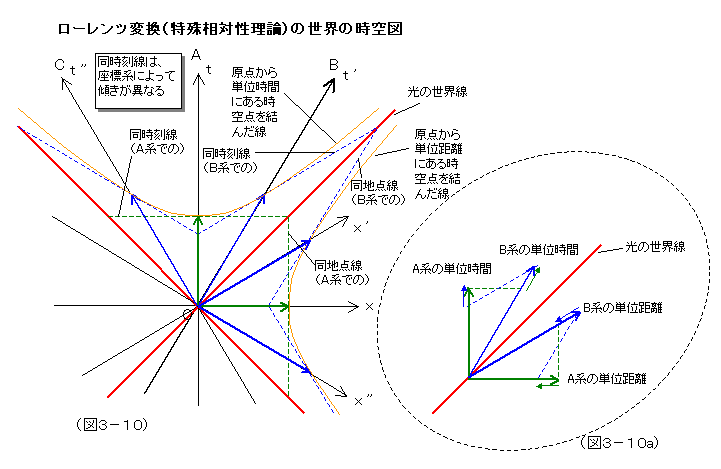
先ほども述べたように、ここでは、同時刻線(空間軸)の傾きが、座標系によって異なるというのが、第一の特徴である。それによって、光速が一定値を保てるわけだ。次に注目すべき点は、空間軸が傾いているために、単位距離を表す空間ベクトルは、先ほどの旧来型時空図と違って、ぴったり重なり合うことはない。単位時間を表す時間ベクトルと光の世界線を軸に対称的になる形で、座標系によって、時間方向に傾きが変わるのである。ここが第二の注目点だ。
そして、単位を表す長さは、どの座標系を基準にしても、一定ではない。先ほどの斜交系であることからくる間延びを補正しても、なお、B系の単位時間は、A系のそれよりも長くなっている。それと同様に、A系の単位時間は、B系のそれよりも長くなってもいる。分かりやすいように、図3-10aに、A系、B系の単位ベクトルの部分だけを取り出してみた。同時刻線は、両ベクトルの中間で交差するように、なっていて、互いに、相手の単位時間が長くなる関係にある。それゆえ、互いに相手の時計は遅れるのだ。
まったく同様のことが、空間的にも言え、B系の単位距離は、A系のそれよりも長くなっている。それと同様に、A系の単位距離は、B系のそれよりも長くなってもいる。「時空的に」言えば、そうなのだが、我々は、事物の判断を、同時刻の断面での構造において行う。つまり、(ある座標系の)ある時刻において、それはどうなのか、という判断の仕方をする。それに従えば、相手の単位距離は、互いに縮んでいるということになる。
もし、旧来型時空図で考えていたように、例えば、ある直交座標系の単位時間、単位距離を基準にして、すべての座標系の単位時間、単位距離はそれに等しいとしたらどうなるであろうか。それについて、図解したのが、次の図3-11と図3-12である。
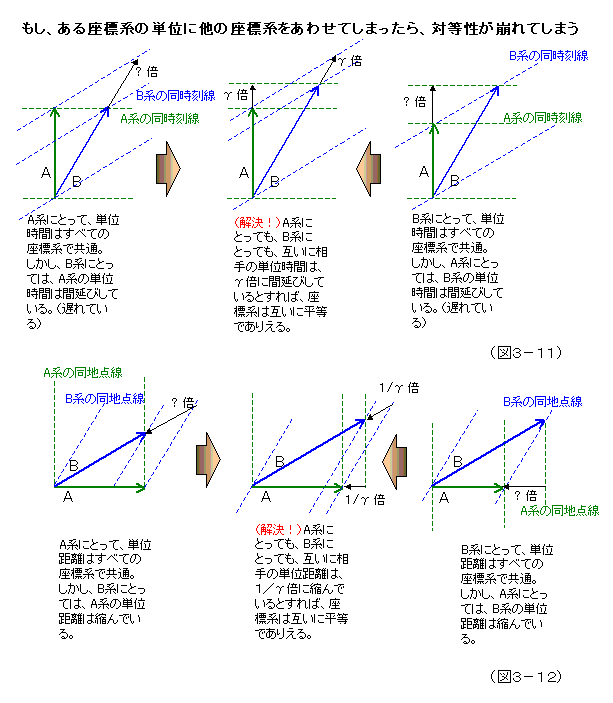
仮に、もし、図3-11の左図のように、A系の同時刻線を基準に、この系での時間と同じテンポで、すべての座標系は時を刻むとしてみよう。つまり、単位時間は、すべての座標系で共通だとA系の立場から宣言するわけだ。これは、旧来型時空図での考え方そのものである。だが、そう考えると、同時刻が相対的であるため、不都合な事態が生ずる。A系で決められた単位時間と同じ時間はどうかと、B系の同時刻線を基準に考えると、先ほどのA系の単位時間は、間延びしていることに、つまり、A系の時計は遅れているということになってしまう。
では、逆に、図3-11の右図のように、B系の同時刻線を基準に、単位時間を定義してしまったらどうなるか。今度は、A系から判断すると、B系の単位時間は間延びして、その時計は遅れているということになってしまう。
どちらを基準にとっても、結局、基準に採用した慣性座標系が特別扱いされてしまうことになる。これは、ガリレイ以来の物理学の基本である相対性原理に反することになる。すべての慣性座標系が互いに同等であるためには、結局、図3-11の中央図のように、互いに相手の系の単位時間は、同じ割合だけ間延びしている、つまり同じだけ、互いに相手の時計は遅れ合っているという関係を想定する以外にないのである。この共通の割合を γ としよう。この値は、二つの座標系間の速度が大きいほど大きな値になるような、座標系間の速度vの関数になっているはずだ。実はこれは、先の3-(1)節で示した、
γ = 1 / √(1-(v/c)2)
に他ならない。なぜかは、このすぐあとでローレンツ変換を幾何学的に導くところで説明する。
図3-12は、空間距離の単位について、先ほどの時間単位と同様の考察を示したものである。互いに相手の単位距離が同じ割合(γ)で間延びしている(ただし、今度は同時刻ラインで判断するから同じ割合(1/γ)で縮んでいる)と考えないと、座標系間の対等性が保てないのである。旧来型時空図では、空間の単位ベクトルは、ぴったり重なっているから、こんなことは、まるで考える必要はなかった。だが、空間軸は傾くようになったため、時間単位と同様に単位距離の座標系間の不変性は保ちえなくなったのである。
ところで、ここでは、時間と空間とは、光の世界線を軸に対称となるような時間・空間の単位系で考察しているわけだから、時間の場合の間延び率 γ と、空間の場合のそれとは、同じ値と考えてよい。
さて、ここで、例のローレンツ変換を時空図から幾何学的に求めてみよう。図3-13を見てもらいたい。ここでは、時間、空間の単位は光速が1となるようなものを採用しているものとする。β=v/c は、座標系間速度を光速との比の値で表現したもので、値は-1~1の範囲をとる。
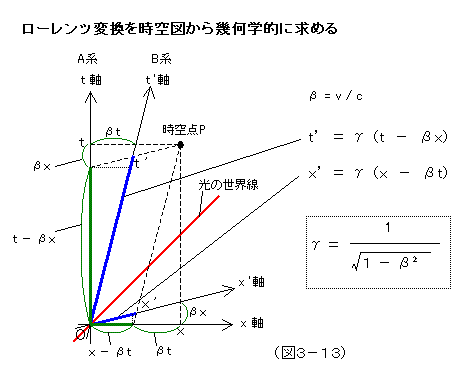
ある時空点Pがあり、それをA系で表現した座標が、(t,x)、B系で表現したものが(t’,x’)である。
A系 → B系 への座標変換では、
時間座標については、同時刻の相対性の効果で、位置が離れるに従って時刻がずれていくため、
(t - βx) というガリレイ変換にはない式が登場し、さらにそれに、γ 倍の効果を考えて、結局、
t’ = γ (t - β x) ...[1]
空間座標については、当然ながら、時間とともに位置がずれていくわけで、
(x - βt) というガリレイ変換と同じ変換式が考えられる。ただし空間軸の傾きのため、γ 倍の効果があり、結局、
x’ = γ (x - β t) ...[2]
B系 → A系 への座標変換では、互いに慣性座標系同士は対等な関係だという前提を考えれば、先ほどの変換式に対して、座標系間速度vの符号が逆なだけと考えればよいから、
t = γ ( t’+ β x’) ...[3]
x = γ ( x’+ β t’) ...[4]
が、考えられる。他ならぬ、先の3-(1)節で示した、ローレンツ変換式である。[1]式か[2]式に、[3]式と[4]式を代入して計算して解いていくと、 γ がどんな関数式になるかが求められる。結果は、先ほど示した通りである。
(ここのところは、拙稿「相対性理論と同時刻の相対性」(三 ローレンツ座標変換)でも、説明したので、数式の展開を確認したい方はそちらを参照願いたい。)
相対性理論において考えられている時空は、単位ベクトル長が、互いに γ 倍になるような計量構造をしているのである。そして、座標軸の傾きが光の世界線に近づいていけばいくほど(速度が光速に近づくほど)、この γ は値が大きくなっていくから、単位長は長くなっていく。原点から等しい時間または距離にある時空点を結んだ線は、双曲線の形になる。(図3-10に示したオレンジ色の曲線。)この双曲線が、(特殊)相対論的時空計量の大きな特徴である。一方、ユークリッド空間では、原点から等距離にある点の軌跡は、円(2次元)や球面(3次元)なわけで、こちらは馴染み深い。ちなみに、時空図では、斜交系での空間における原点から等距離の軌跡は、楕円や回転楕円体で表現される。もっとも四次元の全体像は我々の頭ではイメージとして思い描けないから、その「切り口」が回転楕円体というのは、論理上の想定でしかないのだが。
さらに、この単位長の γ 倍は、エネルギーと質量との等価性(いわゆる有名な E=mc2 )とも深く関係している。(拙稿、「重力を思う (落ちて行く実感からの一般相対性理論)11.4次元的な質量(エネルギーと運動量の統合)」参照) γ 倍効果は、相対論全体の骨格部分とも言えるくらい重要なものなのである。
以上は、論理的要請としてこう考えなくては、宇宙の自然な原理である相対性原理や、等方性(座標系の速度、向きによって物理法則が異なってしまうようなことはないという原理)に反してしまうという根拠で、説明してきた。でも、これだけでは、単なる思弁哲学である。もちろんこれが、物理理論として受け容れられて定着しているのは、この理論に基づいて予測した結果と実際の観測結果とが、ことごとく一致しているからに他ならない。言い換えれば、相対性原理や、等方性の仮定は、これまでのところ、観測によって反例が示されたことはなく、指示されつづけているということである。
indexへ
4.光時計の時空構造
「同時刻の相対性」、「時計の遅れ」、「距離の収縮」、たった、これだけの事柄をこんなにも馬鹿丁寧に説明した本もサイトもそう多くないんじゃないだろうか。が、執拗にもまだ続く。
上記の相対論的効果について、2章では光時計による論理によって、3章では、ミンコフスキー時空図によって解説した。時空図で説明すれば、それは、世界像の提示であり、それを心情的に納得するかどうかは別として、少なくとも論理的には、より鮮明になったはずだ。「光時計による論理」との最大の違いは、「互いに」遅れている、縮んでいる、ということが、一度に鳥瞰できるということではないだろうか。「光時計による論理」では、一方の立場から考えてこう、相手側も対等だから立場を変えても同様にこうなるはず、と、別々に説明されてしまい、全体として両者の立場の相互関係がどうなっているのかが分かりにくい。しかし、時空図を使えば、両者のあり方がストレートに眺望できるのである。
普通はまあ、このテーマはここらで終わって、次のテーマに進む。しかし、それでは、なんとなく気持ち悪さを伴って半信半疑で聞いていた光時計による説明は、何だったのだろうということが置き去りにされてしまう。それで、今度は、光時計による相対論的効果の説明を、ミンコフスキー時空図で再確認しておくことによって、さらにすっきりさせようと思う。
光時計による「同時刻の相対性」の説明の時空的裏付けは、3章で、すでに紹介した。次に時空的に再確認しなくてはならないことは、例の、「時計の遅れ」の説明に使われた、斜めに進む光についてである。
3章において、時空図による、時計の遅れ等の説明は、空間軸はx軸だけ、つまり、1次元の空間のみで説明した。よって、時空図は、2次元でよかった。ところが、斜めに進む光について考えようとすると、空間は少なくとも2次元必要である。(座標系間の進行方向に垂直な方向は、速さ成分が零だから、速さに長さが影響を受けることはない、という洞察にもとづいて、座標系間で共通の距離単位を取得するために必要であった。)
光時計の総体を捉えるには、空間を2次元取った3次元の時空図中の3次元立体で、これを表現しなくてはならない。立体を紙面とか画面とかのような2次元媒体で表現する伝統的な手法は、設計図などに使われる、正面図、平面図、側面図である。これに鳥瞰図をつけておけば、分かりやすくなるだろう。それが、図4-1である。ここでは、図の、A系を静止座標系、B系を運動座標系として説明する。
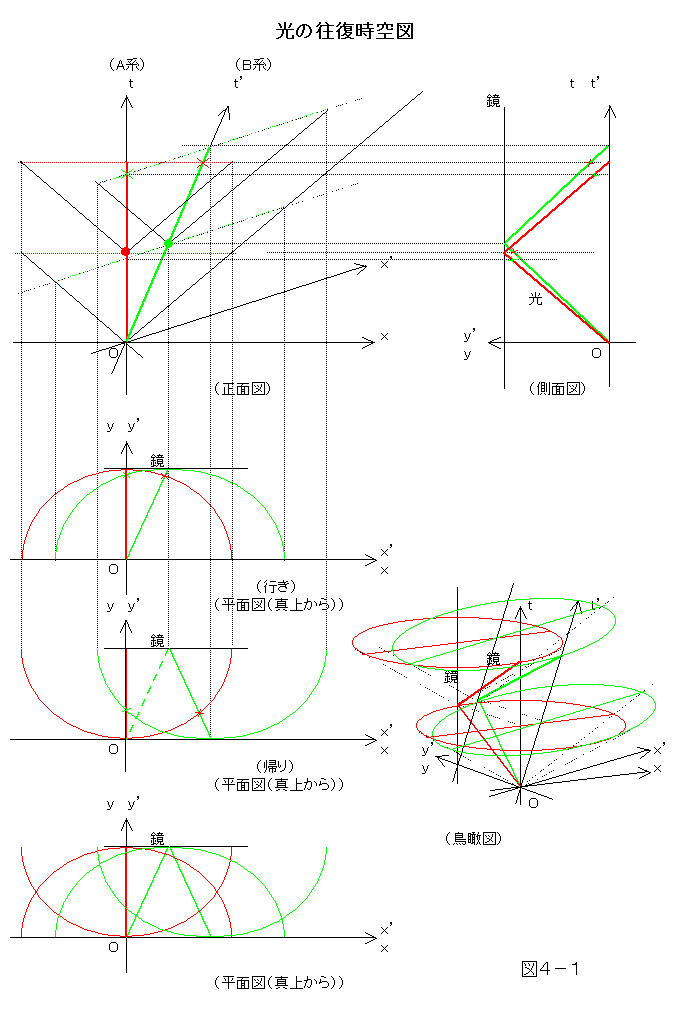
まず、右下の鳥瞰図を見てもらって、どんな立体図なのか、おおよそのイメージを掴んでほしいと思う。ここでは、3つの光円錐が描かれている。一つは、下側の光円錐面で、ある時刻の、ある光源(これを静止系と運動系共通の座標系原点Oとする)から放たれうる光の世界線の集合を表している。この光円錐面上で頂点から引かれたある直線(母線)は、ある方角に向う光の世界線である。赤い世界線が、静止系の鏡に向っていくもの、緑の世界線が、運動系の鏡に向っていくものを表している。この光円錐は、二つの「断面」で切られている。赤い断面が、x軸とy軸を含む平面(x-y面、(以下同様))に平行な、静止系の同時刻面で、その時刻は、静止系の鏡に光が到達した静止系での時刻である。緑の斜めの断面は、x’-y’面に平行な、運動系の同時刻面で、その時刻は、運動系の鏡に光が到達した運動系での時刻である。
上側には二つの光円錐がある。手前の赤い方は、静止系で、光が鏡に到達した時空点を頂点としている。赤い断面は、x-y面に平行な、静止系の同時刻面で、その時刻は、静止系の観測者の位置(光源の位置)に光が戻ってきた静止系での時刻である。もう一方の緑の光円錐は、運動系で、光が鏡に到達した時空点を頂点としている。緑の斜めの断面は、x’-y’面に平行な、運動系の同時刻面で、その時刻は、運動系の観測者の位置(光源のあった位置)に光が戻ってきた運動系での時刻である。以上、立体図の構造イメージはだいたいはわかってもらえただろうか。静止系でと運動系でとの光時計の比較の話は、その実体としては、こんな時空立体が対応しているのである。
それでは、左上の正面図から見てもらおうか。この3次元の時空立体をt-x面で切って見た構図である。(その平面への射影。)これは、前章で、再三、相対論的効果の説明に使われてきた図だ。互いに相手の時間単位(=光が垂直方向(y軸方向)にある鏡まで行って反射して戻ってくるまでの時間)が、間延びしている様子が如実に示されている図である。この3次元の時空立体の本質を表現したアングルだと言えるだろう。(図で、●印は、鏡に反射した時刻を表している。×印は、それぞれ座標系を基準にした単位時間の終端が相手の単位時間中のどの時点に相当するかをプロットしたものである。)
次に、側面図。この3次元の時空立体をt-y面で切った構図である。もし、ニュートン力学の前提に基づいた時空図なら、この側面図に表れる静止系の光の世界線(赤)と運動系の光の世界線(緑)とは、ぴったり重なり合うはずである。両者がずれているのは、まさに同時刻の相対性があるからだ。なお、この側面図は、x軸に平行な視線に基づく角度で見たものなので、緑が上、赤が下になる。運動系(緑)の単位時間が、静止系(赤)の単位時間より間延びしていることが表現されている。もし、この時空立体をx’軸に平行な視線に基づく角度で見上げて、t’-y’面で切った構図としての側面図を描いたとすると、緑が下、赤が上と、上下関係が逆転する。この場合は、静止系(赤)の単位時間が、運動系(緑)の単位時間より間延びしていることが表現されていると言えるだろう。
最後に、平面図。この3次元の時空立体をx-y面で切った構図である。先程の鳥瞰図を真上から見下ろした形だ。上から、(1)光が鏡まで到達するまで、(2)鏡から反射して戻って来るまで、(3)両者を併せたもの、と三通り描いてある。例によって、赤が静止系での光の往復、緑が運動系での斜めに進む光の往復を表している。赤の円は、光源もしくは鏡から発した光が向こう側に到達した時刻と同時刻に光が到達しうる地点を全方位的に示したもので、時空立体の光円錐の切り口に当たる。一方、緑のx(x’)軸方向に間延びした楕円は、運動系でのそれを表現している。
これが、従来より、光時計による時計の遅れ等の説明に用いられてきた図である。このアングルからだと、同時刻の相対性、つまり、空間軸の傾きが分からない。緑の楕円は、傾いているのだが、この角度からではそれが分からない。第2章(2)で、示したように、論理的な推論で、時間の遅れを説明はできるが、それの本質的な根拠である「同時刻の相対性」を、この図からは、読み取るのは難しい。また、相互に相手の時間が遅れ合っている関係にあることを読み取るのも難しい。
かれこれ伝統的に用いられてきた、光時計による時間の遅れの説明は、実は、光の往復過程を示す時空立体を、この最も分かりづらい角度から眺めて考察したものだったのである。このことは、巷に、よく呑み込めなくて、混乱して、あげくの果てに、相対性理論を否定してニュートン力学的な世界像に引き戻そうとする怪しげな「新理論」まで展開しだす人が出てきてしまうような事態を招く、一つの要因になっていると考えられないこともないかもしれない。
以上で、光時計による相対論的効果の説明を、ミンコフスキー時空図で再確認できただろうか。これは、使用する空間次元が2次元なので、時空図は3次元的立体を用いなくては表現できない。だから、やや複雑なのだ。しかし、空間が3次元フルに使われてないから、なんとか、我々がイメージできるモデルを対応させることができた。完全な4次元時空モデルは、もはや図示はできない。数式を使った表現などを頼りに解析していくしかない。
なお、速度の合成則についての時空図を用いた解説が、当サイトに掲載した「相対性理論と同時刻の相対性」の第4章で、提示してある。合わせて、参考にしていただけたらと思う。
indexへ
5.それでも納得のいかない相対性理論?
以上で、特殊相対性理論の基礎中の基礎である、「同時刻の相対性」、「時計の遅れ」、「距離の収縮」は、論理的には、理解してもらえたのではないだろうかと期待している。
相対性理論は、少なくともこの基礎部分に関して言えば、論理として至極難解なものではない。確かに、ニュートン力学よりも基礎部分で、より複雑になってはいるが、ニュートン力学も、応用分野では、ずっと複雑な論理が展開されている。それに、物理学以外の分野でも、これよりはるかに複雑な論理はいくらでも展開されていて、それを多くの人が理解し使いこなしている。相対性理論は、相対的に言って論理としては、決して難しいわけではない。そして、比較的多くの人に関心を持たれていて、解説書も数多く書かれている。にもかかわらず、未だに、基礎部分でその理解の浸透が行き届かず、様々な誤解が横行してしまっているのは、「論理的理解」とは別に、「心情的納得」に至るのに大きな壁があるからではないだろうかと私は思っている。
相対性理論は、時間・空間を扱う。これは、あらゆる分野に基底的に存在する概念だ。単に物理学だけでなく、化学でも生物学でも経済学でも、そして、ごく普通の日常会話でも。それぞれの分野で扱う時間・空間は、呼び名がたまたま一致しているだけで、まったく別の対象を指しているかと言えば、そんなことはない。精度や規模などが、つまり扱い方が異なるだけであって、対象としては、物理学の時間・空間も、日常会話での時間・空間も同じものなのである。物理学で時間が間延びすると言えば、生産にかかる時間も、おしゃべりする時間も間延びするのだ。物理学で時間と空間は4次元の連続体として一体になっていると言えば、それは、各人の人生における時間や生活空間についても、そうなっているということなのである。
時間・空間は、日常的な生活意識のレベルの配下にずっと置かれている。原子や分子に対する思考から離れて生活することは、可能だが、時間・空間に対する配慮を全くしないで生活することは、きわめて困難だ。それで、日常的な生活意識で了解されている時間・空間の観念は、たいへん強烈に我々の意識を支配している。これに矛盾した観念は、実に抵抗が強い。
実際は、矛盾はしてはいない。相対性理論は、日常的な生活意識で了解されている時間・空間の観念を、ある限定された条件、つまり、光速に比べたら殆ど静止しているとみなせるような物体の運動ではという条件のもとでは、常識から隔たったことは何も生じないことを論理的に保証している。だから、論理的には日常的な時間・空間の観念を基礎付けているだけで否定はしていない。むしろ逆に、日常意識の方が、旧来の観念を無条件に通用させていこうとする傾向を持つから矛盾を感じることになる。
そもそも、時間・空間は、我々の認識や論理の形式を基底的に支配している。これは、思考の対象となるに先立って、思考の手段になってしまっているのだ。そして、哲学的思考癖のある幾ばくかの変わり者の思考を除いて、通常、時間・空間そのものが思考の対象になること自体、あまりないことである。そもそも、時間・空間が、形而上学や抽象的な数学ではなく、物理学の対象になってしまうなんてことは、相対性理論以前にはなかったことなのだ。だから、カントは、人類に普遍のアプリオリな形式として固定化した。時間・空間そのものが、発見の対象として、科学の発展に伴って認識の深まりがもたらされていくものであるなんてことは、想定されていなかった。だから、ローレンツもポアンカレも、相対性理論の数式を手にするところまで来ていながら、破天荒なアインシュタインを待つまで新地平には到達できなかったのである。
時間・空間が、我々の認識や論理の形式を基底的に支配しているということは、新たな時間・空間そのものの観念を理解しようとする際にも、古い時間・空間の観念が無意識のうちに紛れ込んでしまいがちになると考えられる。相対性理論に対するあまたの誤解、無理解には、そんな事情で生じているケースが多いのではないだろうか。とりわけ、「同時性」には、注意深い論理的配慮が必要なのだが、それが欠落していて混乱していることが多い。
ところで、このような大きなパラダイム転換を、過去にも人類は、空間について、よく似た状況を経験した。「大地の形状」についての考え方についてだ。
21世紀の今日では、さすがに、大地が全体としてずっと平らなまま続いていて、地の果ては断崖絶壁になっていて、落ちたら地獄だ、なんて信じている人は、よほど公教育から閉ざされた僻地ないし貧困下で暮らすか、特殊な宗教団体に隔離されているかといった特殊事情でもない限りありえない。「丸い地球」という観念は、人類共通のコモンセンスとして不動の地位にある。実際に丸い地球を大気圏外から、あるいは月面から見た人が何人も実在していて、その時の映像も頻繁に目にする。もし、丸い地球を理解していなかったら、単に教養のなさとして人から馬鹿にされるだけではすまさせず、グローバルな経済に基づいた現実の生活に支障をきたすことだって大いにある。そのくらい「丸い地球」は疑いようのない知識になっている。しかし、昔からそうだったわけではない。というか、ここまで大衆的に日常的な常識になったのは、つい最近のことだと言ってもいいかもしれない。
大地が全体として球状をしているというのは、我々地上の動物の身体サイズや行動半径では、あまりにも大きさの規模に違いがありすぎて、直接的に感知できる事柄ではない。人類が地球の丸さを直接見るようになったのは、20世紀後半になってからだし、21世紀の初頭では、まだ、それを実体験している人はごく少数でしかない。大地が全体として球形をしているという知識は、直接的な知覚によってではなく、幾つかの証拠を頼りに論理的に思考して得られたものである。だから、その知識は、長い間、仮説でしかなかった。とは言え、これが論理的に導かれた時代はかなり古い。少なくとも、二千三百年以上も昔のアリストテレスの時代にはわかっていた。船の帆が上から見えてくることとか、月食は、地球の陰であってその形は丸いとかを根拠として、提唱されていた。だが、あくまで、それは学者の唱える仮説であり、多くの人は、永きに渡って、どこまでも大地は平らだと信じていた。
何故なら、もし、球形をしていたら、人や物は、海の水だって、落ちてしまうではないか、というのが、最大の理由だろう。「物は上から下に向かって落ちる。」この上や下の向きは絶対のものであった。「場所によって上や下の方向は変化して行くのであって、一般に物は地球の中心方向に向かって落ちる。その方向を、下と呼ぶ。地球はあまりに巨大であるため、地上に生きる者たちにとって、上下の方向は絶対的であるかのように思えてしまうのである。」という考えは、古代においては、かなり水準の高い理論的思考であると言える。直接的な感覚から得られた概念を、単純に敷衍してしまわないで、直接見ることはできないけれどもより合理的なモデル(球状の大地)を想定し、そこから、逆に直接的な感覚の根拠付けを行うということを行っている。だが、このアイデアが一般的な人々の日常生活世界に取り込まれ浸透していくには、16世紀の大航海時代、その後の列強による世界分割、20世紀に始まる宇宙開発といった時代背景下で、生活世界そのものがグローバルに変革されていく過程が必要だった。
ところで、大地が全体として球状をしているという知識を、ただ単に、昔の偉い学者が言っているのだから、そうに違いないと、受け容れる人もいただろうし、そんな馬鹿なと、あれこれの議論を持ち出して、かたくなに抵抗した人もいただろう。ここで、かたくなに抵抗した人たちの活動は、人類の知識の進歩を妨げる、不要で無意味なものだったという評価を単純に下してしまうべきではないだろう。例えば、なぜ、地表の物体は地球の中心に向かって、落ちるのかを、ただ、そういうものだと無理に納得して終わるより、万有引力の法則というより根本的で普遍的な立場から理解する方向へと発展していく原動力は、過去の学者の権威に頼るだけではない批判精神が支えているだろうから。そこまで大きなことにつながらなくても、とにかく批判的な態度で理論を吸収することは、単純な鵜呑みの態度よりも充実した結果をもたらすことは多いと思う。とは言え、冷静な判断を拒絶して、あるいはかたくなに事実から目をそむけて前に進もうとしないのは、やはり愚かしい限りだ。
さて、問題は相対性理論の四次元時空の場合をこれになぞらえて考えることができるかどうかだ。単なる類推でこれと同じようなことだと語るのは、粗野な論理というべきものだろう。慎重に考えるべきだ。地球の丸さは、はるか上空に上がって見れば、直接的な視覚の対象になりうるものである。我々の銀河系が渦巻き型であることを直接目で見て確かめることは、当面難しいが、原理的には可能なことである。しかし、四次元時空は、どこかに行って、視点を変えて眺めれば見えてくるものではない。これは、原理的に視覚の対象にはなりえないものだ。論理的なモデルとして、思考の対象としてしか、我々は把握できない。ここが決定的に違っている。
では、これは、人間が勝手に頭の中で拵えた架空のもので、実在するものではないと考えてよいか?そう主張している人もいる。しかし、事はそう単純ではないと思う。視覚の対象に原理的になりえないからと言って、それだけで実在性を否定できるような、素朴な範囲に現代の物理学は安住していない。そもそも、電子などの素粒子は、もはや、それ自体が視覚の対象でありうるための波長の範囲を下回っているし、量子力学的不確定性は、およそ、視覚的描像に対応できるものを持ち得なくさせている。だからと言ってその実在性を否定したら物理学ではなくなる。原理的に視覚の対象にはなりえなくても、その実在性を論じることは充分可能なのである。そして、ここでは、視覚ということそのものが、ある巨視的現象であって、非視覚的な物事で、基礎付けられうるものと捉えられる。であれば、四次元時空もしかりであり、これの非視覚性そのものが、物理学的等の事柄で根拠付けられるという方向性も考えられるのだ。
もし、現象学的な観点で、そもそも、こんな四次元時空のようなものは、いわゆる「自然的態度」にもとづくものだから、「括弧に入れて」しまうべきでといった議論を出すとしたら、現象学的な観点そのものの是非は括弧に入れるとしても、少なくともここでは飛躍しすぎだ。そこまで言い出せば、四次元時空どころか、ありとあらゆる物理学的概念が、同列に括弧に入れられてしまうべきで、四次元時空特有の問題点がぼやけてしまう。ここで、問題にしなければならないことは、四次元時空が三次元的な立体としての物体と同等の物理学的実在性を付与しえるかどうかという点なのだ。
四次元時空は、表現上、時間を空間化した形式で提示される。しかし、それをもって、時間は空間と同じものだと相対性理論が主張していると解釈しきることには、慎重でありたいと思っている。時間は空間とは違う。ただ、空間的な表現がある抽象レベルにおいて可能な何かではある。同様に空間もある抽象レベルにおいて時間的表現が可能なある何かなのだ。だが、時間と空間は、明らかに違うものとして我々の意識に現象するなんらかの全体構造が存在しているはずだ。
私としては、四次元時空の実在性は、遠くに実在する他者と同時刻の相対性を考えたとき、肯定せざるを得ないだろうと思っている。それは、当サイトに掲載した「相対性理論と同時刻の相対性」、「同時刻の相対性をめぐる諸問題」で展開してきたので、ここでは多くを述べないでおこう。簡単に言えば、遠くに実在する他者が、こちらに向かっていれば、私の未来部分は実在すると結論せざるをえないし、こちらから離れていけば、私の過去部分は実在すると考えざるをえないのである。
確かに、世界の四次元性を、現代の我々が地球の丸さを常識化しているのと同じくらいのレベルで生活上で実感するには、現代の我々はあまりにも、地表ないし地球近辺でゆっくりとしか移動しない生活形態に限定されすぎている。だが、生活実感は、生活形態に依存して変わりうるものだ。世界の四次元性を生活実感の中に取り込まなくては立ち行かなくなるような時代が到来しないとは、断言できるものではない。
少なくとも、相対性理論を応用してその精度が確保されている、カーナビのGPSは、着実に日常生活に浸透している。光速不変や、それに伴う、本稿で扱ったような基本的な相対論的効果を疑うのは、大地の丸さを疑うことのような陳腐な無理解になりつつある。特殊相対性理論が発表されて、ちょうど1世紀が経つわけだが、確実にその定着度は、高まっているのだ。
ここで個人的な体験を、言うと、私が最初に光速不変を実感したのは、学生時代に測量の補助をするアルバイトをした時だった。古典的な測量は、補助者を測量点に棒を持って立たせて、それをもう一方の測量点から見て角度を測る。これを別の地点からも行い、三角測量の原理を使って、計算で距離を求めるというやり方である。私は、その棒を持って立つアルバイトをしていた。しかし、当時、すでにレーザー光線を使って、鏡に反射させ、その位相のずれから、距離を自動的に計算して表示する機械ができていて、それを使用することもあった。かなり高価なので触るなと言われた。私は、それが使われるときに、決して、地球の運動する方角が気にとめられていないことに留意した。もし、エーテル仮説が正しく、光速が不変でなかったら、こんな装置、使い物にならないと思った。もちろん、そんなややこしい話をしたら、怒鳴りつけられそうだったので、黙ってそう思っただけだけど。まあとにかく、光速不変の原理を否定することは、こんな瑣末な事例も含めて、現代ではあまりにも多くの証拠が揃っていて、不可能である。
ただ、鳥瞰的イメージを抱くことのできない、四次元時空の中での自分の存在とか人生とかをどう考えたらいいのかについては、かなり悩んだ。道を歩きながら、あるいは電車に乗りながら、目の前を通り過ぎる光景を、これは三次元的「断面」なのだと言い聞かせて過ごす訓練をしたこともあった。
四次元時空の実在性、これはいくら考えても、論理的には否定しようのない事実である。私はそう理解している。だが、そのように論理的にこれを理解したとして、これで、完全なる「納得」の地平にたどり着けるか、というと、そう簡単な話ではないと私は思っている。むしろ、それゆえに相対性理論は、やっぱり(心情的に)納得できないという人が出てくるのではとも思っている。
なぜなら、一つには、三次元的物体が運動し変化していく「現在」なるものの流れという、我々の日常的表象は、それでは一体何なのか、という認識論上の問題が上がる。さらに、自由意志はどうなるのか等の倫理学的問題も浮上してくるだろう。
こういった問題にまで深く挑んでこそ、相対性理論は、物理学的、天文学的問題を解くためのツールという地位を越えて、世界観的に納得のいく理論として、身近に引き寄せられるようになりえるのではないだろうかと私は考えている。
ただ、これらは、物理学の範囲内だけでは解決できない。綜合的な考察が必要な課題である。そして、この課題は課題として自覚されてしかるべきだと思う。だが、このような問題の発生を理由に物理理論そのものを否定してしまったり、何の展望もない矛盾だらけの理論をでっち上げたりするのは、問題の解決から遠ざかるばかりの空しい試みである。
indexへ
6.結び
その中で特に混乱と誤解の元凶になっているのが、光時計をめぐっての議論であると思い、そこに焦点を当てて、特殊相対性理論の三大基礎である「同時刻の相対性」、「時計の遅れ」、「距離の収縮」についての説明を試みてみた。私は、相対性理論に対する「論理的理解」と「心情的納得」とを区別すべきだと思っている。後者は簡単ではない課題を含んでいる。だが、前者は、(少なくともその基礎部分に関して言えば)明瞭に到達可能な万人に開かれた地平である。
誤解からは何もまともなものは得られない。まずは、正確に理解すること、哲学的、思想的にどんな立場に立つにせよ、これが共通の出発点である。