「運動する相手の光時計の遅れ」
(The time dilation of the moving Light Clock)
村山 章 (Murayama Akira) 2006年7月
運動する相手の光時計の遅れ率の導出
光時計の光源から出た光は正面にも斜めにも進む。斜めに進んだ光は、移動する鏡に反射して斜めに跳ね返って、移動する光源にぶつかる。これを、この光時計といっしょに移動している人(運動系)は、光は静止した鏡にまっすぐ向かって行き、まっすぐに反射してもとの光源の位置に戻ってきたと観測する。
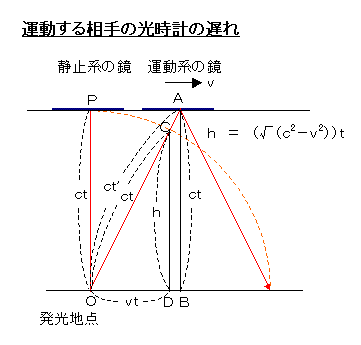
静止系では、鏡までの経過時間を t とすると、距離は、ct である。
一方、運動系では、図で、OAの経過時間が鏡までの経過時間であり、
これを t’ とすると、(光速は不変のcなので、)距離は、ct’ である。
すなわち、運動系の単位時間が経過完了する以前に静止系の単位時間が経過完了
してしまっているわけである。運動系の光時計は、静止系の光時計より遅れていると、
(静止系では)考えねばならない。
ここで、時計の遅れ率(相手の単位時間の膨張率)を γ とする。
t’ = γ t
△OAB ∽ △OCD (相似)なので、
OA : OC = AB : CD すなわち、
ct’ : ct = ct : h
ここで、 三平方の定理より、
h = √((ct)2-(vt)2) = (√(c2-v2))t
なので、
γ = t’/t
= ct / h = ct / (√(c2-v2))t
= 1 / √(1-(v/c)2)
γ ≧ 1 が常に成り立つから、
t’ ≧ t であること、
つまり、運動系での光の鏡までの経過時間は、静止系での光の鏡までの経過時間の
γ 倍に遅れていることが示される。
具体的にvが光速の60%(秒速18万km)の場合だと、(v/c)は0.6で、γ の値は、1.25になる。1.25倍に運動する相手の光時計は遅れるわけだ。
さて、以上の議論は、裏返して、先程、運動系としていた座標系を静止系とみなし、静止系とみなしていた座標系を反対方向に移動する運動系とみなして考えた場合も、同様に成立する。つまり、二つの座標系のどちらか一方が、絶対的な意味で一方的に光時計の進みが遅れるということではなく、互いに同等に、相手側の光時計が自分側から判断すると、遅れていると言い合う関係なのである。