－ アキレスと亀 －
－ ゼノンのパラドックスについての相対論的考察 －(Achilles and the tortoise - A relativistic consideration about Zeno's paradox)
村山 章 (Murayama Akira)
<index>
- はじめに
- 一 アキレスと亀
- 二 相対性原理に基づく「アキレスと亀」
- 三 距離の変化と「分割のパラドックス」、「飛ぶ矢のパラドックス」
- 四 四次元時空の存在
- 五 時間と空間の差異について
- 六 速度の連続性について
- 七 論理は、時間を鳥瞰する
- 八 ゼノンの思想とアインシュタイン
はじめに
実は、私が四次元時空について真剣に考えるようになった、一つのきっかけが、ゼノンの飛ぶ矢のパラドックスでもあった。これを、弁証法的矛盾の実例のようにしてヘーゲルなどは掲げているのだが、私は実在する矛盾、運動の根本原理としての矛盾というものが、さっぱり理解できなかった。ここで登場する矛盾は、単なる対立・拮抗などに対して比喩的意味で用いられているものではなく、正真正銘の論理矛盾なのだ。
論証というのは、一般に矛盾を排除する形で進められる。でなくてはそれは論証になどならない。なのに、最初から矛盾を前提に置いて論じるということは、何なのだろうということが引っかかってしかたなかった。
一方で、時間・空間論に興味があった私は、これを現代的水準で考えられるようになるためには、相対性理論を理解しておく必要性があると思いこれを学ぶようになっていたのだが、そこで、四次元時空という考えがでてくる。四次元時空の観点では、時間は基本的には空間と同質のものとして扱われる。そこで気が付いたのだが、もし時間が空間と同質に扱われたならば、ゼノンのパラドックスは消えてしまわないかということだった。もしそうでないなら、ゼノンのパラドックスは、すべての空間的実在についても言及されねばならず、空間的広がりそのものの実在性を疑問視しなくてはならなくなるが、ゼノンはそこまで主張していたとは思われない。
そんなわけで、すでに展開してあるように、私は四次元時空の実在性について考えるようになった。だが、ここでは、あらためて、ゼノンのパラドックスについて、私なりに考えてみたことを述べようかと思う。まずは、有名な「アキレスと亀」の問題から。
indexへ
一 アキレスと亀
第二の議論はいわゆるアキレスの議論である。すなわち、走ることの最も遅いものですら最も速いものによって決して追いつかれないであろう。なぜなら、追うものは、追いつく以前に、逃げるものが走り始めた点に着かなければならず、したがって、より遅いものは常にいくらかずつ先んじていなければならないからである、という議論である。
（岩波書店：アリストテレス全集３ 自然学 ２５８ページ）
言い換えると、これは以下のような論法である。
アキレスは、亀の後を追いかけている。ある時点に亀のいる地点に、アキレスが到達するとしよう。すると、その時点では、亀は少し前進しているはず。それで、さらにその時点で亀のいる地点に、アキレスが到達すると、その時点でも、やはり亀は少し前進しているはず。従って、これを無限に繰返しても、アキレスは永久に亀に追いつけない。
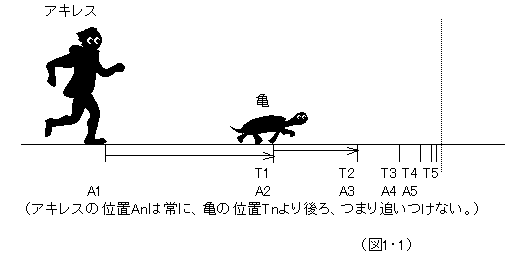
アキレス（ギリシア名：アキレウス）は、トロイ戦争のギリシア軍側のヒーローで、大変足が速かったと言われている。常識的・経験的に言って、アキレスが亀を追い越せないわけがないのだが、ここでは、運動というものがそもそも論理的に立証可能かどうかが問われているのである。
ここで留意すべき点は、アキレスは、速く、亀は遅いということは、言葉では述べられてはいるが、速さとは何か、速いとか遅いとかとはどういう意味なのかということについては何の説明も定義もされておらず、従って、速度とか距離の変化とかの概念はこの論理の中では一切使われていないということである。あくまで、その時点、その地点での到達如何をのみ問題にする形で、議論が進められている。この前提に立って考えると確かに難しいパラドックスのように思えてくる。
よく見かける、模範解答的解決法として、無限等比級数が、一定値に収束することを示すというやり方がある。例えば、アキレスが、（１／２）メートル進む間に、亀は（１／４）メートル、アキレスが、（１／４）メートル進む間に、亀は（１／８）メートル進むという割合でアキレスが亀を追いかけた場合、この過程を無限に繰り返したとしても、アキレス、または亀が進む距離（メートル）は、
（１／２）＋（１／４）＋（１／８）＋（１／１６）＋．．．＋（１／２n）＋．．．
となるのだが、その値は、無限に足しこまれているにもかかわらず、アキレスが亀を追い越す所の１メートルに限りなく近づいていくだけで無限大にはならず、(ある種の演算処理を施せば１に等しいことも示せる)、そしてまた、所要時間についても、アキレスが先に亀のいた地点に行くというその１行程にかかる時間は限りなく零に近づいていくため、一定値に収束していくわけで、結局、これは、アキレスが亀に追いつく限りなく微小に直前のところまでのことを言っているにすぎないのだという説明である。
しかし、これでは、ゼノンのパラドックスの克服にはなっていないという指摘もよくなされることである。ゼノンは、無限の行程が必要とされるような運動というものは、有りえないということが言いたいわけで、それに対して無限の数列の和の性質について論じたところで、論駁になっていないというわけだ。
いずれにせよ、西洋哲学史を貫くようなタイムスパンでこの問題は、論じ続けられてきた。そして、今に至ってもなお論じられている。
時間空間の問題を扱う上で、このような伝統的な問題を無視するわけにはいかないだろう。私も、私なりにこのパラドックスにどう立ち向かうべきか、色々考えてみた。
何が、パロドキシカルにさせているのだろうか。ここの論理に何か誤謬があるのだろうか？ここで、少し発想を変えて、亀とアキレスを、亀１と亀２に置き換えて、考えてみよう。
亀１は、亀２の後を追いかけている。ある時点に亀２のいる地点に、亀１が到達するとしよう。すると、その時点では、亀２は少し前進しているはず。それで、さらにその時点で亀２のいる地点に、亀１が到達すると、その時点でも、やはり亀２は少し前進しているはず。従って、これを無限に繰返しても、亀１は永久に亀２に追いつけない。
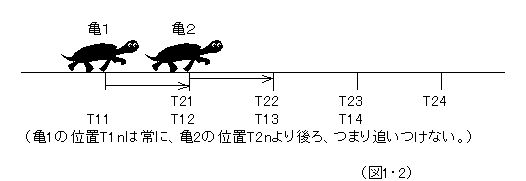
どうだろうか、こう言われたら、なるほど、そんなものかもしれないな、なんて気にならないだろうか。
では、今度は、亀とアキレスを、逆に入れ替えて、考えてみよう。
亀は、アキレスの後を追いかけている。ある時点にアキレスのいる地点に、亀が到達するとしよう。すると、その時点では、アキレスは少し前進しているはず。それで、さらにその時点でアキレスのいる地点に、亀が到達すると、その時点でも、やはりアキレスは少し前進しているはず。従って、これを無限に繰返しても、亀は永久にアキレスに追いつけない。
今度はどうだろうか、こう言われたら、何を当たり前のことを言ってるんだ、なんて気にならないだろうか。あるいは、最初の議論のままでもよいのだが、事前にアキレスというのは、すごいのろまで、亀より遅い、なんて言い聞かされた後で、この論理を読んだらどう思うであろうか。
つまり、ここでパラドキシカルに感ずるかどうかは、論理そのものの中にあるのではなくて、登場する主体、それについて我々が持っている先入観（「アキレスは速く、亀はのろい」など）に関わっていることなのである。もし、このパラドックスを解決しようとして、この論理そのものの誤謬性を見つけ出そうなんて態度で論理分析など始めたら、その時点で、ゼノンのトリックに嵌ってしまったと言えるだろう。
要は、アキレスと亀のパラドックスが示していることは、このような、二者間の「地点」、「時点」の観点のみからでは、追い着き、追い越すといった現象の説明はできないということなのだ。
では、三者ならばどうだろう。
亀の前をナメクジが前進していて、亀はそのナメクジを追いかけているという状態を想定してもらおう。そしてさらにその亀の後方からアキレスが追いかけてくるとしよう。
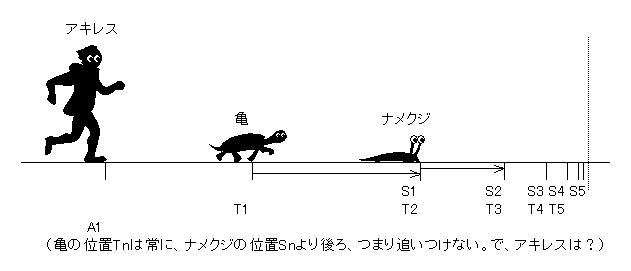
ここで、亀とナメクジとの関係で考えると、先のアキレスと亀の議論と同様のことが言えて、亀は永久にナメクジに追いつけないことになる。これは、よしとしよう。それで、アキレスはどうか？亀が、先程ナメクジがいた地点に到達したその時点で、ナメクジは確かに少し進んでいるから追いつけていないのだが、まさにその時点でアキレスは、亀よりもナメクジよりも前に行ってしまっているかもしれないのである。
ただ、その保証はない。アキレスが追い越すのは、次の時点かもしれないし、次の次かもしれないし、あるいは、やはり永久に追いつけないかもしれない。（亀がナメクジに追いつくまでの時間にアキレスが彼らを追い抜けなかった場合はそうなる。）
アキレスが亀を追い越せるか否かは、論理のみによっては解決不能だ。これは観測に依存する。どこかの時点でアキレスが追い越していたら、それは追い越せたのだと言うことができるのみである。
どうも、「地点」「時点」にのみ執着したゼノンの論法は、実は、追いつき追い越すという現象の解明に対しては、およそ役に立たないもののようである。
indexへ
二 相対性原理に基づく「アキレスと亀」
だが、ガリレオ・ガリレイの出現でその考え方は変えられた。何も力を加えられなかったら、物体は、等速直線運動をするのだ。この考え方は、アインシュタインにおいても発展的に継承されてきている。
それで、このような近代的な観点で、アキレスと亀の問題を考えてみよう。そのためには、地表との摩擦のような複雑な要因を考慮しなくてもいいように、アキレスと亀には、宇宙に行ってもらうことにする。ついでにアキレスと亀を観測するゼノン博士にも宇宙に行ってもらおう。
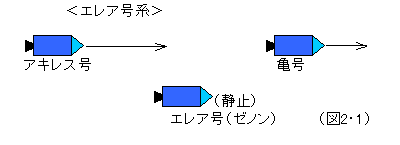
亀田飛行士は、宇宙船亀号に乗って、ゆっくりと地球を離れて例えばシリウスの方向に旅をしている。加速はしていない。はるか後方から、アキレス飛行士が宇宙船アキレス号に乗って亀号を追いかけている。これも加速はしていないが、亀号よりは速く地球から遠のくスピードで、追いかけている。この様子をゼノン博士は、宇宙船エレア号に乗って観測している。エレア号はほぼ地球に対して静止した状態にある。こうしてゼノン博士にも宇宙船に乗ってもらったのは、地球の自転・公転という複雑な条件を考慮しなくてもよいようにするためである。ここで、地球のことは忘れてもらおう。方向を同じくする直線上において運動する（または静止する）３つの宇宙船のことだけを考える。さて、エレア号のゼノン博士は考える。亀号がいる地点にアキレス号が到達した時、亀号はその先を飛んでいる。さらにそこに到達してもやはり亀号は進んでいる。これを無限に繰返しても、アキレス号は、亀号に追いつけない。
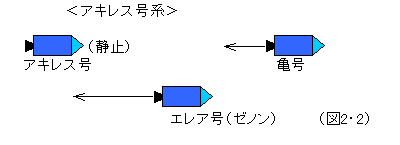
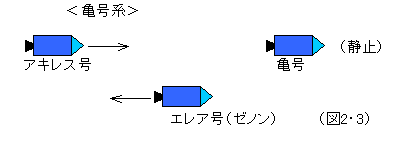
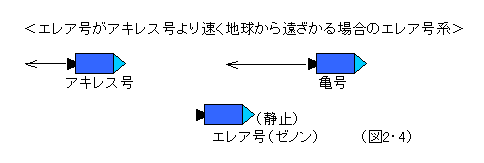
それでは、この状況に対して、アキレス号にいるアキレス飛行士は、どう観測し考えるだろうか。自分はもちろん静止している。エレア号は後方に走り去っていく。そして亀号は、こちらに向かって来る。こう判断する。（図２・２） 一方、亀号の亀田飛行士は、エレア号は立ち去るが、アキレス号は近づいて来る。こう判断する。（図２・３） それだけのことだ。このように自分が静止した基準系で判断すると、ゼノン博士のパラドックスは生まれてこない。あるいはもし、エレア号がアキレス号と同じ速度で飛行していたり、亀号と同じ速度で、飛行していたら、ゼノン博士にとっても、パラドックスは生じない。さらに、エレア号がアキレス号よりも速く地球から遠ざかるように飛行したらどうなるか。今度は、亀号がアキレス号を追いかける状態が発生する。すると、またパラドックスは可能となるが、今度は亀号がアキレス号に追いつけないという話になる。（図２・４） つまり、基準となる座標系次第で、パラドックスは現れたり現れなかったり、逆の形で現れたりするのである。つまり、アキレスと亀のパラドックスは、座標変換に対して不変に保たれない。物理学では、座標変換しても変わらないような関係、性質を本質的なものとして位置づける。このパラドックスは、観測者の座標系に依存した非本質的な事柄なのである。では、座標変換に対して普遍的に保たれるものとは何だろうか。この場合、それは、アキレス号と亀号との距離、およびその変化である。アキレス号と亀号との距離が次第に縮まるという事実は、どの立場からも同じように判定される。（ちなみに相対性理論の場合は、アキレス号と亀号のどの時点をもって距離を計るかが、座標系によって微妙に異なって来るのだが、互いの距離の値は、どの座標系でも等しいことは保障されている。）
アキレスと亀の問題は、両者の距離について言及してこそ、追い着き・追い越しが論じられるのである。ちなみにアリストテレスもこのパラドックスについては、「もし有限な距離を[有限な時間]に通過することを許しさえすれば追いつかれるのである。」と距離について言及することによって論駁を試みている。そもそも、どの地点にいるかということ自体、距離という概念を媒介にしてこそ、厳密に定義できるのである。
アキレスと亀のパラドックスにおいて、空間は、地点の集合、時間は、時点の集合にすぎず、地点間、時点間には、前後関係のような順序関係が定義されうるのみで、距離や時間間隔については定義されていない。ここでは、空間や時間はそういう単純な点の集合にとどまっている。だが、このような集合においては、点と点との距離については言及できないのだ。現代の数学では、物理学的な空間や時空を扱う場合、点は座標で表されるベクトルとして定義され、群論のような抽象代数学による演算関係を用いてベクトル空間を定義する。そして内積の定義を媒介にして、計量ベクトル空間を定義する。（厳密な記述はしかるべき数学のテキストを参考にしてほしい。）つまり、しかるべき構造を持った点の集合として空間を定義しないと運動学を展開できる空間（時空）は得られないということが、現代数学では自覚されている。
重要なことは、アキレスと亀との距離が、どう変化するか、なのだ。もし、その距離が次第に縮まるのなら、アキレスはやがて亀に追い着き、追い越すことができる。もし距離に変化がないなら、同じ速度で追いかけているわけで、永久に追い着けない。もし距離が大きくなっていくのなら、追い着けないどころかどんどん離れていってしまう。
さらに、変化の仕方が一定かどうかも重要だ。最初、距離はどんどん縮まるのだが、しだいに縮まり具合が鈍くなって、そのうち距離が伸びていってしまうような運動をアキレスが行えば、（アキレスが疲れてきて亀より遅くなる、あるいは、反対方向に引き返してしまうような場合）アキレスは亀には追いつけない。当たり前のことで、距離の変化という視点さえあれば、そこには何もパラドキシカルなものはない。
ちなみに、「アキレスと亀」のゼノンの議論は、論理としては、何ら誤謬はない。アキレスと亀との距離が縮まるケースにおいても、両者の間の距離がゼロになる直前において、限りなく正しい。（もちろん空間・時間が無限に分割できるという前提においてだが。）これは、数学的には一定値に収束する無限級数として扱えるケースである。
もし、時間・空間が、単なる「時点」、「地点」の集合であり、計量空間としての定義が与えられていなければ、無限等比級数的な取り扱いも出来ないわけで、ゼノンの「アキレスと亀」のパラドックスは、時間・空間の持つ計量属性の重要性を裏側から指摘したものなのだと理解しておくのがよろしいのではないだろうか。
以上、アキレスと亀のパラドックスは、両者の距離の変化の問題として捉えれば、完全に解決する。これにて、一件落着。
．．．．．．．．．．
indexへ
三 距離の変化と「分割のパラドックス」、「飛ぶ矢のパラドックス」
本当にそうだろうか？いや、実はそうではない。いや、むしろ問題はこれからだと言ってもいい。
ゼノンは、おそらく、ほくそ笑んでこう言うだろう。
「よろしい。アキレスと亀の距離が問題だというなら、それでもよかろう。しかし、考えてみたまえ。アキレスと亀との距離が無くなってしまう前に、その半分の距離になっていなくてはなるまい。さらに、その半分の距離になる前には、さらにその半分の半分の距離になっていなくてはならない。これは、どこまでも無限に言える。つまり、距離が縮まるためには、無限の距離の場合を通過せねばならない。こんなことが有限の時間にできるものかね。結局、アキレスは亀に追いつくどころか、微塵も亀には近づけないのだよ。」
そう、これは、ゼノンの第一のパラドックス、いわゆる「分割のパラドックス」に相当するものである。つまり、「アキレスと亀のパラドックス」は、変化する距離の概念を導入しても、「分割のパラドックス」に帰着してしまうのである。
あるいは、ゼノンはこうも言うかもしれない。
「いいかね、縮んでいる距離は縮んではいない。何となれば、縮んでいる距離も各瞬間には一定の長さの値を占めている。一定の長さの値を占めているものはその瞬間は縮んでいない。ところが、ある距離の状態から別の距離の状態までの時間はその間のそれぞれの瞬間から成り立っている。だがら、縮んでいる距離と言っても、実は縮んではおらんのだよ。」
これは、「縮んでいる距離」を「飛ぶ矢」に置き換えれば、第三の、「飛ぶ矢のパラドックス」である。「飛ぶ矢のパラドックス」というのは、「飛んでいる矢は飛んではいない。何となれば、飛んでいる矢も各瞬間には一定の位置を占めている。一定の位置を占めているものはその瞬間は飛んでいない。ところが、ある矢の状態から別の矢の状態までの時間はその間のそれぞれの瞬間から成り立っている。だがら、飛んでいる矢と言っても、実は飛んではいない。」という話である。つまり、「アキレスと亀のパラドックス」は、「飛ぶ矢のパラドックス」にも帰着してしまうのである。
こうなると、やはり、これまで多く語られてきたように、ここから先は「無限とは何か」、「連続とは何か」について、緻密に論及していくという展開になっていくべきなのだろうか。
ニュートン、ライプニッツらの極限概念、カントールの無限の濃度、デデキントの切断．．．これらは、不思議でやっかいな数、０（零）との格闘の歴史とも言えるのだろう。無限小を無矛盾な公理体系の中に収めるため、近代、多くの論理学的、数学的探求が発展した。
これらの理論構築が多大な価値をもたらしたことは、言うまでも無いことである。ある意味で、ゼノンのパラドックスの価値は、こうした数学の発展を促す一つの誘引にあったのだと評価することもできるかもしれない。しかし、私は、ゼノンのパラドックスの解決を、はたして、無限性、連続性の問題に還元してしまっていいものなのだろうかと思っている。何故なら、無限性、連続性は、なにも、運動、時間の問題に特有の事柄ではないからだ。ゼノンは、空間の広がりまでも矛盾に満ちて認められないとは言っていないように思われる。
もし、連続的な空間の広がりにも矛盾を指摘するならば、空間は存在しない、曲がったものは存在しないなど、およそこの世のすべてを否定しにかからねばならなくなる。あるいは、空間の場合、すべてを離散的な存在の集まりとみなすことも可能である。デモクリトスで代表されるような原子論的考え方である。空間の広がりは、連続を前提しなくても存立可能なのだ。だが、これが、運動・変化するとなると、とたんに連続性が問題になってきてしまう。なぜなら、ある状態から別の状態への移行にあたって、無限にその中間過程を考えざるを得なくなるからである。ゼノンのパラドックスがもたらしている問題提起の本質はこの移行に伴う無限分割にあるのだ。連続性・無限性の問題はこの意味で、運動・変化の問題と強くリンクしていると言えるだろう。
連続性、あるいは無限性というのは、それ自体を計測して確かめることは、原理的に不可能である。もし出来たら、それは無限ではないことになる。これは、論理的に考えられる対象でしかありえない。つまり、終局、限界点と言ったものを想定できないが故の論理的要請によって措定された概念である。ゼノンは、その点をこそ、強調したかったのではなかったのだろうかと私は想像する。現実問題として、無限なんて実現できやしないのだからと。
indexへ
四 四次元時空の存在
四次元時空では、運動する点は、一本の世界線と呼ばれる線となる。運動する円盤は、一本の棒であり、運動する球体は、一本の超円筒というか、我々にはイメージ不可能なある種の四次元立体になる。そして、（ここが重要なのだが）ここにもはや運動はない。もし世界線などが運動するものだとしたら、今度はさらに超時間を考えなくてはならなくなるが、その場合は五次元時空を考えれば、運動はなくなる。ただ、我々は、一次元より多い時間の次元を考えなくてはならない必要性に迫られていないので、三次元の空間と一次元の時間を合わせた四次元時空を考えれば充分なのである。
この四次元時空を、単なる便宜的な仮想の概念的構築物にすぎないと捉えるのか、三次元空間と同じように実在する世界の抽象モデルと捉えるのかで、これからの議論が意味をなすか否かが決まってくる。この点は大変重要なのだ。もし、時空が仮想のものにすぎないとすれば、四次元時空を基礎にしたゼノンアポリアの解釈は、ほとんど説得力を持たないと思われる。だが、三次元空間と同じくらいに実在性があるとするならば、これからの議論は、充分、注視する価値がある。ちなみに、三次元空間もそれ自体としては、抽象概念の一つにすぎないわけで、その意味でなら、四次元時空も当然、概念的構築物である。しかし、三次元空間は、我々は実在世界の客観的なモデルとしてごく自然に受け入れており、それと同等の実在性が、四次元時空に与えられうるか否かが問題なのである。単なる便宜上考えられたグラフにすぎないのかどうかということなのである。
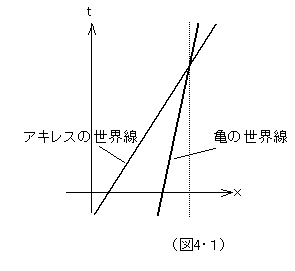
ということで、世界は、四次元なのだ、という前提で、議論を進めよう。すると、アキレスと亀のレースはどう捉えられるかというと、アキレスと亀をそれぞれ空間内の点として抽象化するならば、それは、傾きを異にする二本の世界線となる。アキレスの世界線と亀の世界線が交差した所が、アキレスが亀に追いついた瞬間の時空点である。
「飛ぶ矢」はどうなるか。四次元時空の中に、飛ぶ矢の世界線が存在している。それに尽きるということだ。飛ぶ矢と平行な時間軸を持つ座標系（つまり飛ぶ矢と同じ速度で移動している観測者）以外の基準からは、飛ぶ矢が運動していることは一目瞭然である。
「まず、世界線ありき」というこの観点では、少なくとも存在論的には、無限に中間過程を実現することをしなくても、運動は完成されているのである。運動の始まりから終わりまで、そのすべての過程が確定して存在しているのだ。そこに、無限の数の生成局面が連ならなくてはならない理由はない。四次元時空における四次元立体や世界線は、それ自体としては生成も消滅もない。運動、生成・消滅、発展・衰退、それらすべては完成されたものとして存在しているわけであって、運動が何故可能かなどと問う余地はないのである。少なくとも、空間的広がりが何故あるのかと問う余地がないというのと同じ程度において。
そして、三次元的な「断面」の運動や、生成・消滅、発展・衰退という様相は、すべて、世界を認識する側の持つ形式に由来するのであり、我々（この「我々」に、人間を超えたどの範囲までが含ませられるかは難しい問題ではあるけれど）の認知能力の属性として、言い換えれば、一種の共同幻想として解釈する必要がある。すると、何故、このような表象として認識主体には世界が把握されるのか、という問題は残る。
この問題は、さらに稿を改めて論じるべきだろう。とにかく、四次元時空の考えは、無限分割を媒介にしないで運動するものの存在を基礎付けられるということ、ここでは、まずその点を強調しておきたい。それこそ、映画のフィルムのように、世界が時間的に離散的な存在形式であったとしても、運動する存在そのものは揺るがないのだ。運動すること、即ち、四次元時空幅を持って四次元世界に存在することなのである。「静止」とは、その対象を構成する世界線が互いに平行な構造をもった四次元物体を、それと時間軸が平行しているある座標系から見た特殊な表現をさしているに過ぎないのであり、静止はこれもまた運動（＝四次元存在）の一形式であって、運動と根本的に対立する概念ではなくなるのである。
indexへ
五 時間と空間の差異について
いわゆる「時間の流れ」の問題は、奥が深く、もとより簡単に論じきれることではないのだが、ここでは、相対性理論が明らかにした四次元時空構造そのものから、時間と空間の差異性がある程度導けるということを、次の二点の疑問に答える形で、提示してみようと思う。
＜疑問その１＞
何故、ある一時点（これは厳密な幅のない点ではなく、ある幅をもって考えてよい）において、空間は広がりのあるものとして捉えられるのに、時間は「今」と呼ばれる局在化した形式でしか認識されないのか、つまり過去から未来までのある広がりとして事物が認識されることがないのか？
＜疑問その２＞
何故、空間的には、同じ地点に戻って来られるのに、時間的には、同じ時刻に戻って来られないのか？
この四次元時空構造とは、ミンコフスキー時空を線形的な基礎とした、リーマン時空なのだが、ここでは、重力場で、歪んだ状態は考慮しないで、単純なミンコフスキー時空で考えれば充分である。この四次元時空は、三次元の空間と一次元の時間で、成り立っており、簡単のため、空間次元を一つ減らして描いた図で考える（図５・１）。
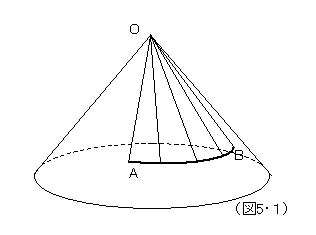図で、原点Ｏは、現在の認識主体を表しているとしよう。曲線Ａ－Ｂは、空間的に広がった時空点（事象）の集まりである。それぞれの事象からは、原点Ｏに同時に届くような情報を伝達する伝達手段が存在する（例えば光）。つまり、空間的な隔たり（広がり）は、それを同時把握することが可能な構造が現実に存在しており、故に我々は、空間を広がりのあるもの（延長のあるもの）と認識することが、現実に可能なのである。
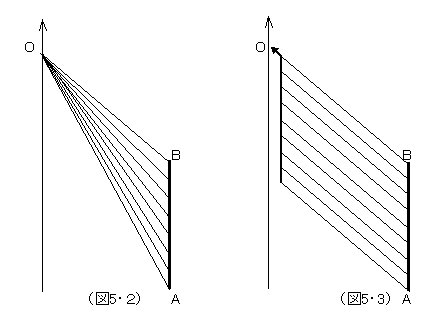ところが、一方、時間はどうだろうか。図５・２の世界線Ａ－Ｂは、時空内に時間的に広がった時空点（事象）の集まりである。そして、原点Ｏは、現在の認識主体を表している。ここに、同時に届くような情報を伝達する伝達手段が存在するだろうか。これが、可能であるためには、徐々に連続的に速度を異にする光のような伝達手段が各事象から発せられて、認識主体は、より遠い過去のものはより遅い伝達手段、より近い過去のものはより速い伝達手段を選択して構成するというとてつもなく複雑な処理をしなくては、世界線Ａ－Ｂ上に時間的に広がる事象を同時に認識することはできない。しかし、現実には、このような連続的に速度を異にする伝達手段など存在していないし、そもそも、より近い過去からきたものなのか、より遠い過去から来たものなのかの判定をどうするのかと言う問題にもぶつかり、およそ不可能なことである。あえて考えられるのは、図５・３のように、受け取った情報を暫く溜め込んで、まとめて認識するような、遅延認識機構を認識主体が持った場合、認識主体は、時間的広がりを、一度に把握できるかもしれない。コンピュータ・グラフィックスの世界で、こんな仕組みを実現して、奇妙な映像を楽しんだりしている例はあるけれど、現実の生物界には、このような能力を持ったものはいない。もし出現したとしても、このような懐古趣味的機能が生存競争に有利に働くとは思えないから生き残れなかっただろう。つまり、我々の認識においては、空間的広がりは、一時点で把握できるが、時間的広がりは、できないということは、そのように、時空構造そのもの、並びに認識機構が成り立っているということで説明ができるのである。
なお、ここで付言するならば、情報の伝達方向は、一方的であり、未来から過去に向かって情報が伝達されることは（少なくとも巨視的なレベルで、我々が知る限りの宇宙では、）ないことになっている。もしこれが可能になると、因果律に重大な問題を引き起こす。これも、何らかの時空構造がもたらしていることではないかと思われる。（「時間の向き」の問題については、これはこれで、独立して論じるべき大きな問題である。このテーマについて、最近、手にして興味を引いた本に、ヒュー・プライスの「時間の矢の不思議とアルキメデスの目」というのがあって、大変内容が濃い。ここで展開されている時空観は、やはり、四次元時空の前提としており、私の主張してきたことと通じるところが多いような気がする。）
では、次に、「疑問その２」について。
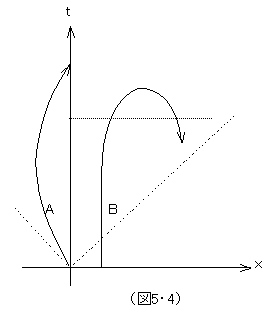図５・４で、描かれる二本の曲線は、時空点の連続体である世界線である。まず、曲線Ａについて。この世界線は、左側に向かって行き、途中で引き返して元の地点に戻ってくる世界線である。（元の地点が何かは、座標系に依存するけれど。）当然、こういう世界線は、現実の四次元時空の中にごく普通に存在している。一方、曲線Ｂはどうか。未来方向に向かう世界線は、ある時点で引き返して過去に向かう。このような世界線は、現実の四次元時空には存在しえない。何故なら、このようなことが実現するためには、世界線Ｂは、光速の壁を突破し、無限大の速度からマイナス無限大の速度を経て、さらに超光速から光速以下になるという経緯を辿らなくてはならないのだが、そのようなことは不可能であることを相対性理論は示している。空間的に行ったり来たりは出来ても時間的に行ったり来たりは出来ない最大の理由は光速の壁なのである。それに、世界線Ｂのような形をしたものが仮に存在できたとしても、外部の通常の観測者からは、これは、離れた二つの物体が速度を増しながら近づいて行き、光速を超えて無限大の速度で衝突した瞬間に、跡形もなく消えたとして観測されるだろう。もちろん、このような物理現象は観測されてはいない。
あと、補足的に述べるが、この世界が四次元だと言っても、数学的に抽象的に考えられる四次元ユークリッド空間ではない。四次元ユークリッド空間ならば、あるべきはずの四次元幾何学的性質が、我々の世界であるミンコフスキー四次元時空では見られないということが幾つかある。
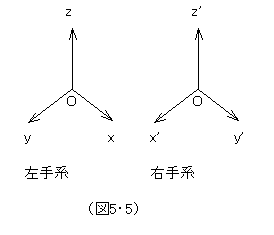
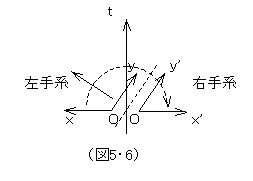例えば、図５・５で示す、左手系（ｘ－ｙ－ｚ）と右手系（ｘ’－ｙ’－ｚ’）は、三次元ユークリッド空間内で、どんな回転＆平行移動を行ってもぴったりと重ね合わせることはできないが、四次元ならできると言われている。分かりやすく、二次元で説明すると、、図５・６で示す、左手系（ｘ－ｙ）と右手系（ｘ’－ｙ’）は、二次元平面内で、どんな回転＆平行移動を行ってもｘとｘ’、ｙとｙ’を重ね合わせられないけれど、三次元空間を使って「裏返す」という回転移動を行えば、重ね合わせ可能なのである。同様にして、三次元的に重ね合わせ不可能でも、四次元空間を使って「裏返」せば、重ね合わせられるはずだということは、数学的に言われていることなのだが、現実には、右手を左手に取り替えてしまうなんてことはできない。これも、やはり、光速の壁が出来なくさせていると考えてよいだろう。図５・６で、裏返すような回転移動を行うには空間軸を反転させるように傾けなくてはならないが、空間軸の傾きはせいぜい、光速を表す傾きに近づけることしかできない。相対性理論が提示する、現実のミンコフスキー四次元時空では、単純なユークリッド四次元空間に比べて、回転移動に制限が与えられているのである。我々の意識にとって、空間と時間は、明らかに、質的に異なる。だが、意識に現れるがままに、客観的な空間や時間のありようもその通りなのだと信じるのは、ナイーブすぎやしないだろうか。色が、物体そのものの属性と単純に結論できないように、直接的な認識事実を素朴に実態の属性として決め付けてしまうべきではない。それが、科学的批判的近代精神が培ってきた基本姿勢である。空間と時間は、同質の四次元時空の異なる断面にすぎないけれど、その幾何学的構造から、質的に異なるように意識されるにいたるのだという説明は、充分可能なのだ。
しかし、ここで述べたことで、この問題が語り尽くせているとは思っていない。
一体、何故、意識は、過去と呼ばれている方向から、未来と呼ばれている方向に、時空をスキャンしていくようなあり方として発現しているのだろうか？ 正直、よくわからないのだが、それでも、はっきり言える（言いたい）ことは、「時の流れ」は、四次元時空内における、意識の発現形式なのだという捉え方をするべきだろうということである。時の流れの中の意識が四次元時空を概念的に構築したという捉え方をする人もいるだろうけれど、私はこの立場を取らない。
indexへ
六 速度の連続性について
実際、物理学の歴史は、原子の発見、量子論の確立に見られるように、概念的には、連続したもの、無限分割可能なものだと考えられてきた物質やエネルギーが、構造的に最小単位を持っていることを暴き出してきている。それで、当然、時空そのものも、非連続で、量子化されうる何かではないかということは、考えられるわけだ。それが現代物理学の目指すべき目標として掲げられていることも、しばしば目にする。
相対性理論は、とりあえず、三次元の空間と一次元の時間を統合した四次元時空で立論されているが、現代物理学は、さらに高次元の時空モデルを用いて、統一理論を模索している。超高密度エネルギー（質量）下での超微細構造に言及した場合、どこまでも四次元モデルに拘泥しているわけにはいかない。ただ、通常のマクロ的条件下では、四次元モデルで事足りるような具合に理論モデルは構築される。四次元性そのものも条件的であって、より普遍的にはもっと高次元の時空モデルが成立しており、特定の（我々には馴染みの深い）条件下でこそ、通常の四次元性は、充分な構造モデルたりえるに過ぎないのだという形で理論モデルは進化し続けている。（超弦理論では、十一次元の時空連続多様体が考えられている。）
相対性理論、というより、近代以降の物理学の根底にある基本前提は、同等の条件下であれば（例えば歪みのない時空での慣性系であれば）、すべての座標系は互いに同等であって、なにか宇宙に特権的座標系や原点というものが存在しているわけではないという考えである。宇宙はみな平等であって、今、我々の立つ視点のみが全宇宙の中で特別なのではない、これは、天動説から地動説に移行して以来の、基本的な考え方であって、この先、この前提が覆されることは、まず考えられない。
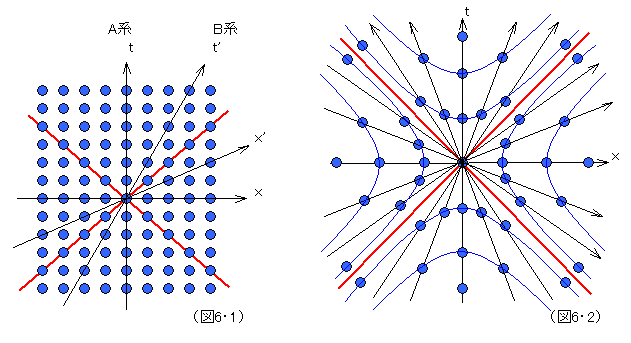
その上で、時空の離散モデルを考える。図６・１は、単純な格子状の離散モデルである。四次元世界は、超微視的にはこのような離散構造をしていると仮定してみよう。ここに、互いに速度を異にする二つの慣性座標系Ａ系とＢ系を考える。すると問題が起こる。Ａ系では、時空要素４つが経過する間に、Ｂ系では２つしか経過しない。もっと一般的に考えても、この格子状離散モデルは、異なる慣性座標系間で対等でない。
それでは、ミンコフスキー時空構造を加味して考えた、図６・２のような時空離散モデルでは、どうだろうか。この場合、原点から等距離、ないし等時間にある時空点を結んだ軌跡は、双曲線を描く。この双曲線に沿って時空要素が存在していると考えた場合、速度を異にするどの座標系からも、時空要素の存在する密度は、同等になる。つまり、原点を共有する座標系間でのローレンツ変換（速度変更）に対して、不変の構造だと言える。しかし、このモデルでは、原点から遠ざかるに従って、時空要素の密度が疎らになってしまう。言い換えると、アフィン変換（平行移動）に対しては、不変な関係を保てないのだ。これは、ある時点のある地点が宇宙の絶対的中心であると考えねばならないことを意味しており、このような時空離散モデルは、やはり受け入れがたい。
このように、素人レベルで考えても、時空の離散モデルは、単純には成り立たない。時空の連続性は、そう、簡単に捨てられるものではないのだ。実際、量子力学について考えてみても、全てを単純に離散化したわけではない。何故なら、量子力学の方程式が扱う（観測前の）「状態」は、ｎ次元複素ベクトルで表されるわけで、複素数は、連続濃度をもった実数と虚数の組合せだから、連続数である。世界は、それほど単純な連続体ではないのと同じくらいに、それほど単純に非連続ではないのだ。
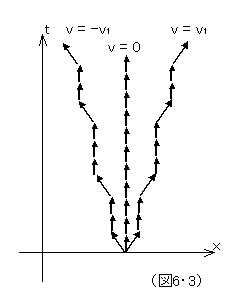
それでは、「速度の連続性」についてはどうなのだろうか。図６・３は、非連続速度モデルの一例である。非常に微小なある究極的単位時間という仮定をし、その時間においては、速さ（速度の絶対値）は、零（静止）か、ある一定値（例えば光速）のいずれかしかありえないとする。実際の具体的な速度はこの二種類の速さの適当な組み合わせで実現されると考える。この時間単位は非常に微小であるために、マクロ的には、あらゆる速度が連続的に可能であるかのように現象すると考える。このモデルは、ミンコフスキー時空構造に矛盾しないで立論可能であろうか。絶対的な時空要素の離散配置を想定する図６・２の場合と違って、時空の長さ（固有時間／固有距離）の量子化なので、特定の原点を特別視する必要はなさそうだ。しかし、そもそも、究極的微小単位時間という考えが可能なのか、また、世界線のある部分が、どちらの速度要素であるかを任意の座標系で一意的に保てるのか、そもそも、速度も観測されない限り、不確定なある量子状態にすぎないのではないか、まあ、素人レベルで考えててなんとかなるほど簡単な問題領域でないことだけは確かなようだ。
ただ、この節で、私が、提示してみたかったことは、四次元実在世界観のもとでは、時間・空間の連続性、あるいは速度の連続性は、運動というものを成り立たしめるための要請として現れるのではなく、座標系間の同等性の要請など、別の次元からの要請として現れるということである。運動は生み出されるものではない。それは認識主体の観念形式であって、運動は、存在しているのである。
ここで、「速度の連続性」ということで、やはり、想起されるのは、最後に残ったゼノンの「競走馬のパラドックス」であろう。（これについては、「時間のパラドックス」（中村秀吉・中公新書）Ｐ166などを、参考されたし。）
これは、同じ長さの静止した物体と移動する物体とがすれ違う時間と、互いに反対方向に移動する同じ長さの二つの物体がすれ違う時間とが等しいという、今日の相対運動についての常識からして明らかに誤っているとしか思えない前提で立論されているので、黙殺されることが多い。だが、これについて、中村秀吉氏は前掲書で、時間と空間の最小単位という前提で考えると、このパラドックスのパラドックス性が明白になり、このパラドックスの誤りは時間・空間を大きさを持つ最小単位の合成と考えたことにあると指摘している。
このパラドックスをどう評価するべきかについては、色々な意見があるのだろうが、とにかくも、時間・空間の量子化問題さえ思い起こさせるような考察までもゼノンが残していたことに、私は少なからぬ驚嘆の念を抱かずにいられない。
「連続性は、実在の属性なのか、論理思考の要請によって観念の中に築かれたものにすぎないのか。」この問題は深く長く続く哲学的アポリアの一つである。
indexへ
七 論理は、時間を鳥瞰する
本稿は、ゼノンのパラドックスを足がかりに、時間と論理の問題を考察していくことがテーマである。ここで、あらためて、論理というものが、時間というものにどう対峙する関係にあるのか、考えてみたい。
さて、ある命題が正しければ、その対偶命題も正しいという論理法則がある。例えば、「人間であるならば、動物である。」という命題が真であるならば、「動物でないならば、人間でない」は正しい。前提と結論のそれぞれを否定して逆にした命題を対偶と言うが、これは、元の命題と真理値を等しくすることが分かっている。論理学のごく初歩的段階で学ぶことである。
それでは、命題「しかられないならば、勉強しない。」について考えて見よう。これは正しいとしよう。すると、この対偶命題は、「勉強すると、しかられる。」となり、これも正しいはず。。。。え？なんか、変だぞ。
実は、これの正しい対偶命題は、「勉強したなら、（その前に）しかられた。」である。ちなみに、「投資しなければ、儲からない。」の正しい対偶命題は、「儲かれば、投資する。」ではなく、「儲かったなら、投資していた。」である。投資しなければ、儲からないからといって、儲かれば必ず再投資してくれることまで、論理学は保証してはくれない。
何が言いたいかというと、そもそも論理というものは、本質的に時間を超越し事象を鳥瞰できる立場にたってこそ成り立つということである。前者の「人間であるならば、動物である。」という命題は、包含関係に関する論理で、基本的に時間を貫いて不変な関係を表している。こういう論理は、対偶を取るような形式変換をしてもなんら問題は生じない。しかし、後者の命題は、因果関係を表している。つまり、前提（原因）と結論（結果）は、時間的に前後していることが暗黙のうちに含意されている。従って、因果関係を表現した命題の対偶を取る場合は、時制に配慮しないと、誤りに陥る。時制に配慮するとは、「今」の束縛から自らを解き放つことであり、任意の時刻に身を置ける、時間を鳥瞰する立場に立つことである。
すなわち、論理とは、時の流れに身を任せていたのでは、成り立たないのである。時の流れの外に身を置いて、時空を鳥瞰しなくてはならない。だから、因果関係の論理を吟味したければ、過去と未来を眺望できる位置にいなくてはならない。力学は、動く物を動くがままに見るのではなく、（関数を用いるなどして、）運動体の軌跡を描く形で、経過を全体として眺望しなくては、微積分学を適用して解析などできない。あるいは、音楽は、ただ感じるままに歌い奏でるならば、時の流れの中に内在していられるけれど、ひとたび、その構成を論理的に吟味しようとしたら、時間を貫いて変わらない楽譜という形式に置き換えないといけなくなる。楽譜は音楽という時間彫刻に対する空間模写である。論理思考が直接対象にできるのは、このような空間化し固定化したものなのである。
ここから、導かれるひとつの教訓というか、留意事項がある。論理は、本質的に物
事を固定化して把握するものであり、それゆえ、変化することへの対応が苦手なので
ある。
なにより、論理の基本構成要素は、名辞、すなわち「概念」である。概念 "concept"は、ラテン語"conceptus"（取り入れること、心に抱くこと）から来ている。ドイツ語の"Begriff"は、"begreifen"（ものをつかむ、把握する）という動詞から派生した。いずれにせよ、自分のところに引き寄せて、ばたつかせないように、押さえ込むというニュアンスが感じられる。つまり、対象をあるがままに自由に羽ばたかせていたのでは、概念にはならないのだ。動かないように固定化させてこそ、それは概念としての地位を獲得できるのである。それでは本質的に動くものはどう概念把握するかと言えば、時間の流れの外に身を置いて時間を鳥瞰するかたちでそれをつかみ取るしかない。
我々は、何故、概念把握や論理思考を行うのか？世界の真理を知るため？それを独立した自己目的にできるようになるのは、ずっと文化が成熟してきてからのことであって、何よりも、我々はまず、生きるために、概念把握や論理思考を行ってきたはずだ。我々は、現象を見聞きし学習し法則性を掴んだ上で、より有利な行動を選択する。これは、ある程度学習能力を備えた動物ならば程度の差こそあれ普遍的に行ってきていることであって、高度な社会組織と言語処理能力を備えた人間は、この戦略を著しく発展させたわけだ。概念や論理は、まず、このような生命活動の所産として、存立しているのであって、世界の真理に到達するために生まれたわけではない。
つまり、過去の知識を法則化して後の行動に有効利用できるような形で世界を把握してこそ、意味があるのである。だが、これは、事物を固定化させることと不可分なのだ。
単純な位置の変化をする運動について考えてみよう。我々は、物体の位置についてまず認識しないことには、そもそも状況認識は微塵も進まないから、物体がどこにあるか把握する。これは、とりあえず位置を固定化させるのだ。「そこにある」として。だが、運動する物体は、時間と共に位置を変える。それで、「別の時間にはあそこにある」とも認識せねばならない。これも位置の固定化認識なのだ。それから、単位時間における位置の変化する割合「速度」という概念に到達する。ところがここでは、速度を固定化させる。が、これでも正確な状況把握には不十分だと判断されると、速度の変化率「加速度」という概念を生み出す。やはりここでも加速度は固定化される。現実には、等加速度の運動なんて、ごく限られた世界でしか起きていないことで、一般的には、位置も速度も加速度も、常に変化して止まないのが現実の世界である。近代の解析学は、極限的な微小構造を想定し、その変化に連続関数を対応させることで、とりあえず実用上問題のない形で、常に変化して止まない現実の世界を把握することにある程度成功した。しかし、その極限的な微小構造そのものを考察する局面では、固定化された概念把握が根底にあるのだ、ということは忘れるべきでない。これは論理思考の宿命なのだ。
そうすると、論理思考にとっては、曲がりくねった現実の四次元世界に直面して、「矛盾」を避けられなくなる局面がでてくる。「そこの位置にあって、そこの位置にない」、「その速度にあって、その速度でない」．．．．．等々。
ヘーゲル哲学からマルクス主義にいたって強調されてきた「弁証法」というのは、これを何かある確立した方法論なり論理学なりのように解釈するよりも、連綿と続くある種の思想運動の形態として解釈した方がいいように私は思っているのだけれど、つまり、宿命的に固定化作用を持っている概念把握、論理思考が常に直面せねばならない現実との乖離という陥穽に対する警鐘運動として「弁証法」を捉えるのが生産的ではないかと。我々は、一度把握した、概念、法則性といったものを、無限定、無条件にごり押ししてしまう傾向がある。だが、現実の四次元世界は、複雑に曲がりくねって入り組んだ構造をしている。それに気づかないでいると、例えば、一連の「社会主義」のように硬直化して自己崩壊を招きかねないことにもなるのだというような警鐘として。
indexへ
八 ゼノンの思想とアインシュタイン
相対論的に見て、万物は一つであるかもしれないが、無数に分割して考えることも可能な局面を多く持つ何かでもある、と言うことも可能だろうし、そもそも、パルメニデスの言おうとしていたことの真意は何で、どんな文脈から、その思想は説かれたのか、詳しいことはもうわからない。だから、こんな議論をしてもあまり意味はないだろう。
ゼノンは、時の圧政者ネアルコス打倒を謀る一味に加わったが発覚し、拷問にかけられた。彼は共謀者の名を明かすと言い、王が耳を傾けた時、その耳に噛み付いて、殺されるまで離さなかった、などというエピソードが伝えられているらしい。そんなことからしても、ゼノンの自らの思想を貫き通そうとするその意気込みには、ただならぬものを感じる。何か我々には知られない深い思想的背景があったのかもしれない。少なくとも、単なる論理的謎掛け遊戯を楽しんでいたわけではなさそうだ。
ただ、私として、気を留めておきたいことは、「万物は一つである、運動はありえない」などという一見なんともスタティックな思想を堅持しながら、彼がかくも大胆な政治運動に身を投じたことである。そのすさまじいまでの情熱は、パルメニデスの思想とどう関わっているのだろうか。それを思想の一貫性のなさと捉えるのか、思想そのものにそれがあったと見るべきなのか。確かに、アインシュタインだって、政治に無縁ではいられなかった。と言うか、いやがうえにも大きく関わらざるをえない状況に彼は立たされてしまった。それは、決して、かれの相対性理論や量子論や統計力学から導き出されたものではない。それと同じで、一定以上の正義感を持ち合わせていたものが、偶然のっぴきならない政治状況に立たされて起きたことにすぎないのかもしれない。そして、そういうことは、あっていいことだ。思想の一貫性を前提してすべての事を解釈しようとするのは、哲学嗜好人間の悪い癖だとも言える。しかしそれでも、そうではなく、その姿勢は彼のパルメニデス思想と深く関連があったという可能性も否定は出来ない気がするのである。もちろん、もはや確かめようのないことなのだけれど。
ともあれ、ゼノンは、彼の投げたパラドックスによって、数千年の長きに亘ってその名を残すこととなった。その真意は謎のまま。
戻る