A PHILOSOPHY OF THE FOUR-DIMENSIONAL SPACE-TIME
The Worldview of Relative Simultaneity (MURAYAMA Akira)
CHAPTER II The Problems of Continuity and Contradiction
First and foremost, this chapter focuses on the famous paradoxes of Zeno of Elea (500-430 B.C.).
It was Zeno's paradox on a flying arrow that inspired me to pay keen attention to four-dimensional space-time. Georg Wilhelm Friedrich Hegel (1770-1831) regards this subject as an illustration of dialectical contradiction, but I could not make sense of the idea of an existing contradiction, contradiction as a fundamental principle of movement. The contradiction referred to here is a real logical contradiction, not a euphemism for mere confrontation and antagonism.
Generally, an argumentation is conducted by removing contradictions; otherwise arguing about and demonstrating a subject would be impossible. That is why I was uncomfortable about the argumentation based on the assumption that there are some contradictions.
In the meantime, I was interested in the space-time argument. I had thought it necessary to understand the theory of relativity to approach the argument at a contemporary level and had educated myself about the theory of relativity. During my study of the theory, I faced the concept of four-dimensional space-time. In accordance with this concept, time is basically treated as having the same quality as space. If time is treated as basically having the same quality as space, then Zeno's paradoxes may be invalid. If the paradoxes are valid, they should all be referred to as spatial existences and we have to be skeptical about the existence of spatial expansion itself. Zeno did not argue to such an extent.
As mentioned in chapter 1, that is how I came to consider the existence of four-dimensional space-time. In this section, I present my ideas about Zeno's paradoxes with a focus on the issue of continuity and contradiction, one of the important issues concerning time.
I first note the famous paradox about Achilles and the Tortoise. In mentioning the paradox, I highlight that its logic focuses on certain points of space and time and shows that the concept of distance is essential. However, the introduction of the concept of distance does not completely demonstrate the specifics of Zeno's paradox and essentially, examination of the concept of being infinitesimal is inevitable. In this analysis, I examine the concept from the vantage point of four-dimensional space-time without using conventional number-theoretic approaches to the infinitesimal. Based on this approach, I raised problems on the relationship between logics and time.
According to the concept of four-dimensional space-time, space and time are treated the same, but the two are clearly different. Here, I approach the origin of the differences between space and time from a geometrical perspective. However, I do not think that my examination is convincing enough. My argument still leaves mysteries on our time representations. I will examine time representations in the next chapter.
As an important subject in this chapter, I note the fact that the existence of four-dimensional space-time makes time continuity unnecessary for realizing movements and changes. I am also skeptical of declaring that time continuity is just a conceptual model based on our thinking and not an existing attribute. This is because examinations on velocity suggest the necessity of time continuity from a different angle.
1. Achilles and the Tortoise
In Physics Aristotelēs (384-322 B.C.) argues to refute Zeno's ideas.
The second theme is the Achilles argument. That is, the argument maintains that even the slowest runner will never be overtaken by the fastest runner. This is because the chaser always has to reach the spot where the chased runner started to run before catching up. In accordance with this reasoning, the slower runner (the chased runner) needs to move ahead, little by little, of the faster runner (the chaser).(*1)
This story can be interpreted as follows. (The slower runner referred to here is traditionally interpreted as the tortoise and the faster runner is Achilles.) Achilles is running after the tortoise. When Achilles reaches a certain spot where the tortoise existed at a certain point in time, the tortoise must be a little ahead of Achilles. Achilles moves on to get to the spot where the tortoise is and the tortoise must be a little ahead of Achilles again this time. Endless repetition of this chase makes it impossible for Achilles to catch up with the tortoise (See Figure 2-1-1).
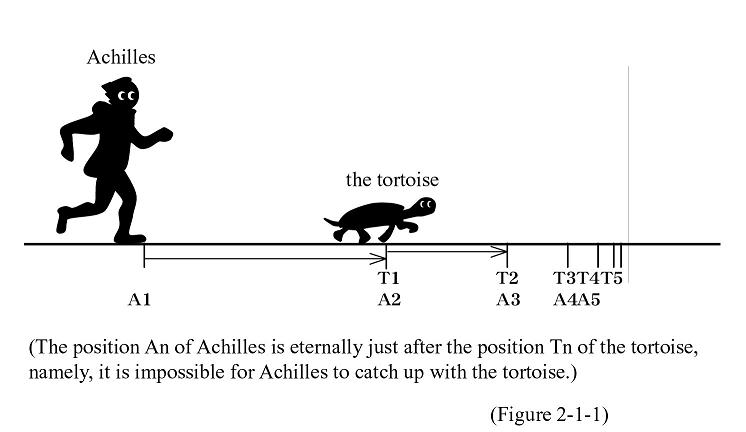
Achilles, in Greek Achilleus, was the Greek hero in the Trojan War around 1,200 B.C. and is reputed to have been a very fast runner. Our empirical knowledge tells us how natural it is that Achilles can easily overtake the tortoise, but the point here is if movements are logically demonstrable.
Although Achilles is described as faster and the tortoise as slower, no clear meaning or definition of fast or slow is provided. Therefore, the concept of changes in velocity and distance is not involved in this argument. The argument is based on a certain spot at a certain point in time. Thinking based on this assumption makes the argument seem a difficult paradox.
A frequently-presented model answer to this question is the way to show its infinite geometric series converged on a certain value. Suppose the tortoise moves one-fourth meter while Achilles moves one-half meter and the tortoise moves one-eighth meter while Achilles moves one-fourth meter. Suppose that this process is endlessly repeated. The distance covered by Achilles or the tortoise can be obtained as follows:
Although the value is endlessly added, the distance just gets close to a one-meter position, where Achilles overtakes the tortoise, and never shows infinity. If you conduct a certain type of calculation, you can obtain a value of 1. In addition, the time necessary for one process for Achilles to reach the spot where the tortoise existed approaches almost 0, and converges on a particular value. This explains the situation just before Achilles catches up with the tortoise in their infinitesimal race. Zeno did not recognize the infinitesimal concept, which was established by modern differential and integral calculus.
However, many point out that this examination does not work to overcome the contradictions of Zeno's paradoxes. Zeno's argument was based on the assumption that there could be no movements requiring infinite processes. Discussing the nature of added infinite sequences does not lead to counterargument. This subject has been discussed throughout Western philosophical history.
We cannot ignore this traditional long-discussed issue when we examine issues concerning space and time. I also deliberated on how to approach this paradox. The two questions are what makes this subject paradoxical and if there are any erroneous factors in the logic. Next, I change perspectives. I examine the subject by switching Achilles and the tortoise to Tortoise 1 and Tortoise 2.
Imagine a situation in which Tortoise 1 is chasing Tortoise 2. When Tortoise 1 reaches a certain spot where Tortoise 2 existed at a certain point in time, Tortoise 2 must be a little ahead of Tortoise 1. Tortoise 1 goes on to get to the spot where Tortoise 2 is and Tortoise 2 must be again a little ahead of Tortoise 1. The endless repetition of this chase makes it impossible for Tortoise 1 to catch up with Tortoise 2 (See Figure 2-1-2).
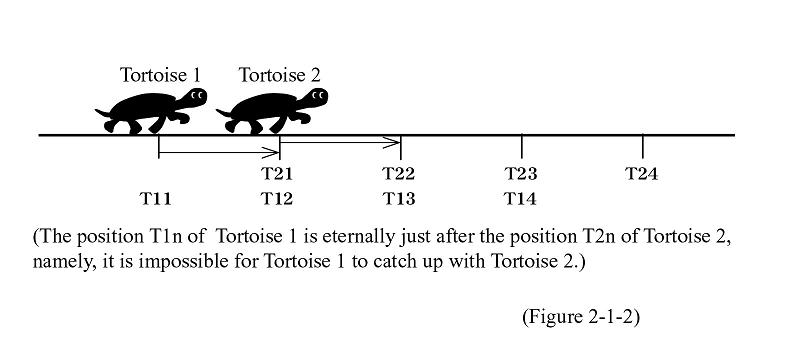
Now the two questions are what you think about the new scenario and if the switching convinces you. Next, let me reverse the positioning of the tortoise and Achilles.
The tortoise is chasing Achilles. When the tortoise reaches a certain spot where Achilles existed at a certain point in time, Achilles must be a little ahead of the tortoise. The tortoise goes on to get to the spot where Achilles is and Achilles must be again a little ahead of the tortoise. The endless repetition of this chase makes it impossible for the tortoise to catch up with Achilles (See Figure 2-1-3).
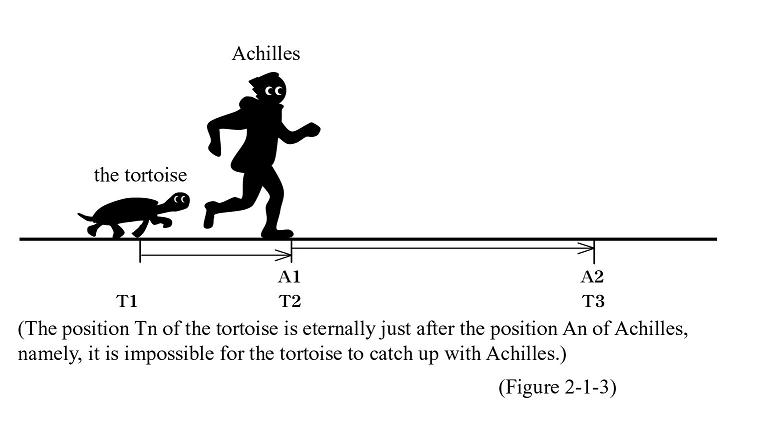
The two questions now are what you think about this and if you think it natural that the tortoise can never catch up with Achilles. Or if you are informed in advance that Achilles runs more slowly than the tortoise on the basis of this argument, in which Achilles is running after the tortoise, the question becomes how your reaction to the logic.
The point is that what makes you realize the paradox in this story depends not on the logic itself but on Achilles and the tortoise and our preconceptions about them. That is, Achilles is a fast runner and the tortoise is a slow runner. If you analyze the logic to find its erroneous factors in an effort to solve the paradox, then you will fall into Zeno's trick.
In short, the paradoxes about Achilles and the tortoise suggest that the phenomenon of catching up with or overtaking the other cannot be explained from only the perspective of the positioning and the points of time between the two.
Then, the question is how the scenario would be with three actors. Now, imagine a situation in which a slug is moving ahead of the tortoise, which is chased by Achilles (See Figure 2-1-4).
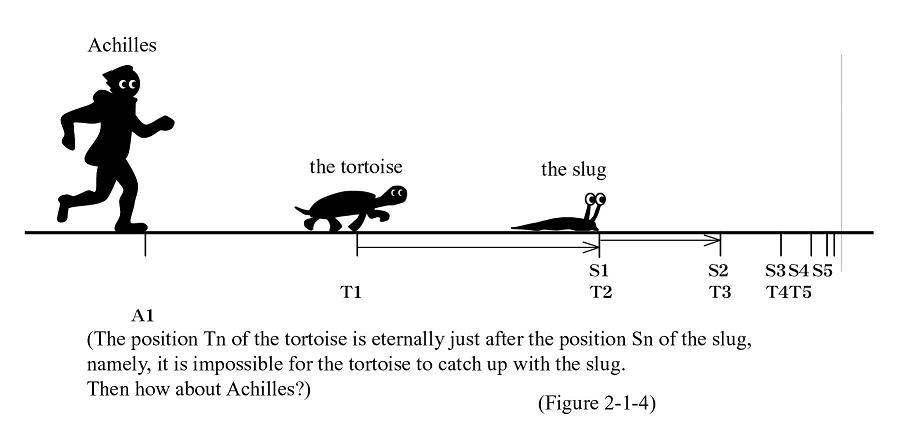
With a focus on the relationship between the tortoise and the slug, the tortoise can never catch up with the slug, just as the earlier relationship between Achilles and the tortoise has shown. The question is what will happen to Achilles this time. When the tortoise reaches a certain spot where the slug existed at a certain point in time, the slug must be a little ahead of the tortoise. The tortoise cannot catch up with the slug, but it is possible that Achilles will be ahead of the tortoise and the slug at this very moment. However, this is not always true. Achilles may overtake the tortoise the next moment or the next moment after or he may be unable to ever catch up with the slug or the tortoise. (This case may occur in the situation where Achilles cannot catch up with either of them before the tortoise catches up with the slug.)
Whether or not Achilles can overtake the tortoise cannot be handled only by logic. This depends on observation. Only when Achilles catches up with the tortoise at a certain point in time does Achilles overtake the tortoise.
Zeno's logic focusing only on positioning and points in time seems useless for examining the phenomenon of catching up with or overtaking someone or something.
(*1) Refer to Aristotle, Aristotle’s Corpus III: Physics, translated by Takashi Ide and Chikatsugu Iwasaki (1968), Iwanami Shoten Publishers, p. 258.