「双子のパラドックスについて」
(The Twin Paradox)
村山 章 (Murayama Akira) 2004年10月 執筆
<index>
-
1.はじめに
-
2.双子のパラドックスとは
-
3.特殊相対性理論の概要
-
4.双子のパラドックスの様々な解法
-
5.千代島氏の「哲学的批判分析」
-
6.二人は離れ、そして再会する - その場合分け
-
7.物理理論の中の循環論法について
-
8.ミンコフスキー時空図は発明か発見か
-
9.結び
1.はじめに
ここでは、このパラドックスを通して、物理学の理論の捉え方というものについて、考えてみたい。物理学においては、(物理学に限らず、一般に科学全般についても言えるだろうが、)ある論理モデル体系が提起されて、それが、観測される全ての現象を、統一的に説明できうるかどうかについて追求され、想定される範囲で、それが成功すれば、(さし当り)正当な理論として認可される。相対性理論はそのような形で認可されている理論の一つである。ただ、提起された理論は、それ自体としては大変抽象性が高く、分かりにくいものであるし、そのままでは利用もしづらい。従って、物理理論は、その応用や、解説などをするにあたり、具体的な状況に合わせた特殊化を施して、提示される。
「双子のパラドックス」も、その一つで、(典型的かもしれないが)ある特殊な状況を想定し、その状況下で、生じる現象を、理論的に説明していくことなのである。
ところが、ここで、この特殊化された説明論理を不用意に一般化して再解釈し、少なからぬ議論の混乱を招くことがある。いわゆる「オルタナティブ」の物理学を提唱しておられる論者(「とんでも系」とかとも言われている)も、往々にしてこのケースに嵌まってしまった場合が多いのではないだろうか。「双子のパラドックス」は、21世紀初頭の我々の生活実感からは、経験できなくて、また、相対論的な時空概念に馴染まない状態では、なかなか納得し辛い現象を扱っているから、具体的な説明が強く要求され、またなされてきたわけだが、それとともに、混乱した再解釈も後を絶たないようである。
ここでは、まず、普通の(いわゆる正統派の)物理学者による「双子のパラドックス」の説明として、松田卓也・木下篤哉共著の「相対論の正しい間違え方」(丸善)での展開を例に紹介し、次に、そのような物理学者の説明に対して、いわゆる「哲学的批判分析」を与えている事例として、千代島雅著の「アインシュタイン「双子のパラドックス」の終焉」(徳間書店)を挙げて、その内容を吟味してみようと思う。この本はあからさまに「相対性理論は間違っている」と主張している系のものではなくて、微妙なのだが、それだけにしっかりと批判しておかないといけないと思った。
その上で、私は、双子の宇宙飛行の一般論を提示し、一般と特殊の関係(一般相対論と特殊相対論という意味ではない)という視点で、私なりの「双子のパラドックス」の解説を試みてみようと思う。つまり、弟が地球に残り、兄が宇宙旅行をするというのは特殊ケースとして捉える。そして、兄も弟も共に宇宙旅行して再会する場合を一般論とし、それで両者の時間経過はどうなのかを問うという形で展開してみる。
その上で、物理理論を我々はどういう姿勢で捉えていくべきかについて、私なりの考えを述べてみようと思う。
最後に、ミンコフスキー時空をどう評価すべきかについて、千代島氏の考えと対比する形で、私の見解を述べる。
indexへ
2.双子のパラドックスとは
双子の兄弟がいて、あるとき、兄は宇宙船に乗って宇宙に旅立ち、そして、再び、地球に戻って来て弟と再会する。だが、相対性理論の効果によって兄の時間の進み方が遅くなったため、兄はまだ若いのに、弟は老人になっていたという話である。
これが、実際に実在する人間の双子によって、実験して確かめられたことは、21世紀初頭の現在ではまだない。ただ、時間の遅れという相対論的効果についての実験的検証は、数限りなくなされてきていて、上記のような現象は、間違いなく実際にありうることだと言われている。
では、これのどこがパラドックス(論理矛盾)なのか、ということなのだが、両者が双子であるにもかかわらず、一方だけが年を取ってしまったことがパラドックスなのか、というと、そういうことが、パラドキシカルなわけではない。地球上の生活での常識では不思議なだけであって、それ自体はパラドックスとは違う。一方の年の取り方が遅かったらこういうことになることは、何も論理的な矛盾を含んでいない。
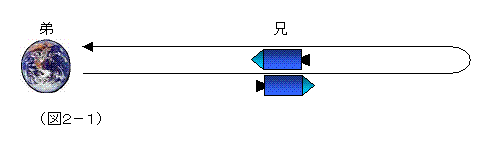
では、何がパラドックスなのかというと、それは、運動の相対性に関わることである。そもそも、運動(場所の移動)というのは、ある基準(何に対する移動なのかの何)があってこそ、語れるものであり、その基準は任意のものであってよく、絶対的な運動の基準系などない。これは、近代の力学が、明確にしてきた確固たる認識である。宇宙船に乗った兄が移動したというのは、地球にとどまる弟の座標系を基準にした場合に言える事であり、兄を基準にすれば、地球に留まっている弟の方が遠く隔たり、そしてまた、兄の宇宙船に近づいてきたという過程として表現される。つまり、兄からすれば、自分は静止しており、弟の方が運動(離れて、近づくのだから加速度運動)をしたと言えるわけで、だとすれば、弟の方が年の取り方(時計の進み方)が遅くて、出会ったときは、自分の方が老人で、弟はまだ若いと言えるのではないか、ということになる。同じ時間と場所で二人は出会うわけなのに、弟からすれば、兄の方が若く、兄からすると、弟の方が若いと言うのは、明らかに論理矛盾である。これが、パラドックスと言われるゆえんである。
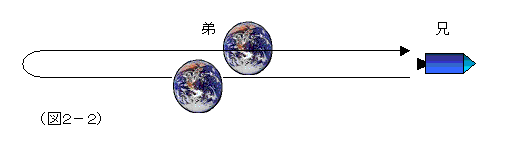
特殊相対性理論では、互いに相手の時間の進み方は遅れているということが言われる。この場合は、論理矛盾ではない。特殊相対性理論は、等速直線運動する座標系間のことを記述した理論で、それぞれの座標系に乗ったものは、再び顔を合わせることはないから、互いに相手の時間の進みが遅いと判断していても、問題は生じない。
だが、行って戻って再会するとなると、問題が生じる。どちらの側からも、どちらか一方が年を取っているか、ともに同じだけ年をとっているかでないと、客観的な真実はないことになってしまう。
過去には、これゆえに相対性理論は、間違った理論だという議論が、よくなされていたようである。もちろん、相対性理論は、明確な解答を与えている。地球から遠ざかって戻ってくる兄の方が、年の取り方が少ないのである。いずれの座標系から判断しても。
indexへ
3.特殊相対性理論の概要
アインシュタインは、光を伝達する媒質(エーテル)なんてものそのものの存在を信じていなかった。彼は、光速を、宇宙の普遍原理として考えた。何故なら、全宇宙に普遍的であるべき電磁気学の法則がある特権的な座標系だけで成り立つなんてことは容認できることではないわけで、その法則から光速が導かれるのなら、それも普遍的なものと認めるべきだと考えたからだ。だが、速度なるものが異なる座標系間で共通の値を持つというのは、ガリレイ以来の運動学の常識に大いに矛盾する。光速で移動するものを光速の2分の1の速度で追う者からすれば、それは光速の2分の1になるというのが常識なのだが、相対性理論では、やはりそれは光速のままだと主張されるのだ。光速をいくら追いかけても光速のままなのである。彼は、光速は、そもそも速度の限界値、極限値で定数だとした上で、運動法則そのものの方を作り変えた。どんな慣性座標系からも、究極の速度=光速は、一定となるよう、時間・空間の考え方そのものに修正を加えてしまった。そして、ニュートン力学そのものを根底から書き換えてしまったのである。そうすることで、速度の合成は、単純な加減算では厳密に求められるものではないことが示され、上記の常識との矛盾も解決されるのである。
どう考えれば、どんな慣性座標系からも光速は一定とできるか、それは、距離が隔たったものの同時性は、絶対的なものではなく、座標系に依存して相対的であれば、可能なのである。「同時刻の相対性」は光速の不変性を根底で支える基本認識である。
だが、同時性が絶対的なものでなくなると、時間の進み方も、どんな座標系からも同様なものと考えるわけにはいかなくなる。ある座標系(以下、特に断りなければ慣性系)を基準にその座標系での時間の進み方が、すべての座標系にも当てはまる時間の進み方なのだと考えると、とたんに矛盾が生じる。同時性が異なるため、もとの座標系で主張された1時間は、別の座標系を基準にして考えると、1時間に満たない時間だと判断されてしまう。つまり、最初の座標系では、相手の時間の遅れはないのに、別の座標系では相手の時間の進みが遅いと判断されてしまう。慣性座標系は、すべて同等というガリレイ以来の原理に従うなら、互いに相手の座標系の時間の進み方は同じ割合で、遅れ合っていると判断されるような関係であるべきである。
同様のことが、空間的距離についても言及でき、相手の距離は互いに同じ割合で縮んでいると判断されるべきだということになる。以上のような考察から、慣性座標系間の座標変換法則を求めると、ローレンツ変換式が導かれ、速度の合成則はじめとする、数々の相対論的力学の体系が導かれてゆくのである。
(以上のことは、当サイトの第一論文「相対性理論と同時刻の相対性」で、図解してある。)
ともかく、等速直線運動する二つの座標系は、互いに相手の時計の進み方は、遅いと判断する関係にある、これが、双子のパラドックスを考える上での基本前提である。弟にとっては、兄の時間の進み方が遅れ、兄にとっては、弟の時間の進み方が遅れるのである。これは、一見、矛盾しているようだが、矛盾ではない。これが矛盾になるのは、同時性がすべての座標系で絶対的な場合に限る。
この点については、千代島氏も「立場が違うのだから」という視点で、ずいぶん言葉を尽くして、認めている。
indexへ
4.双子のパラドックスの様々な解法
「双子のパラドックスを解く」とは、何故、宇宙旅行をした兄の方の時間の進み方が遅れ、その逆ではないかを、説明することである。
これは、いくつもある。 松田卓也・木下篤哉共著の「相対論の正しい間違え方」では、以下の5種類に分類されて紹介されている。
1)折れ線時空図法
2)相互信号受信法
3)同時線法
4)距離観測法
5)一般相対論的説明
以下、これらを簡単に紹介しておこう。
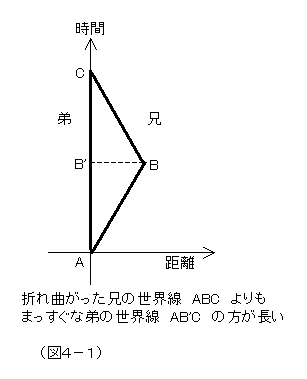
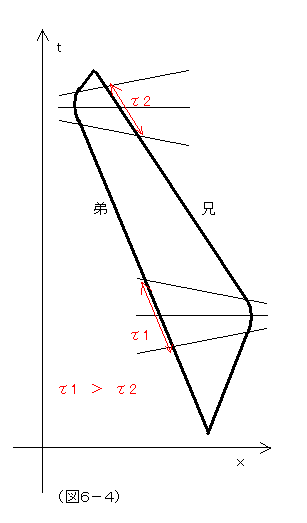
これは、ミンコフスキーダイヤグラムを描き、地球にいる弟の世界線を直線に、宇宙船で行って戻る兄の世界線を折り返し点で折れ曲がる曲線で描いて説明する。実際は、折り返しはある程度なめらかなカーブを描かないと、宇宙船も兄の体も潰れて壊れてしまうのだが、その点は単純化してある。ここでの論拠は、ミンコフスキー時空幾何学における時空計量である。歪みのない平坦な時空(=重力場がない、もしくは無視できるくらい小さい)においては、2点を結ぶ線の「長さ(ここでは固有時間)」は、直線があらゆる曲線に比べて、一番長いということが、幾何学的に導ける。通常のユークリッド幾何学では、直線が一番短いのだが、時空幾何では、三平方の定理が違っていて、距離の2乗は、各成分の2乗の和ではなく、時間成分の2乗と空間成分の2乗の差として定義されているのでこうなる。このように、時空幾何の計量的性質に基づいて、宇宙旅行をする曲がった世界線の兄の固有時間の方が、まっすぐな弟の世界線の固有時間よりも短いと判断するというのが、折れ線時空図法である。本質的な論法で、相対論を幾何学的に理解した人にとっては、シンプルでエレガントな論法である。
2)相互信号受信法
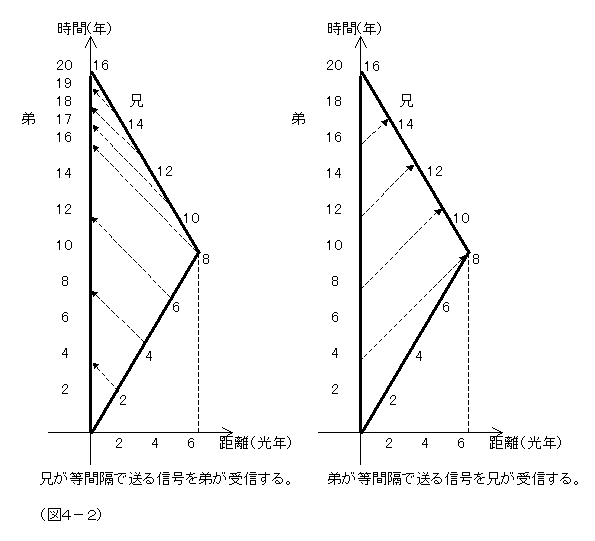
これは、兄、ないし弟が、相手に対し、等間隔で、現在時刻の情報を送信し続けることを想定して、例えば、兄は光速の60%の速さの宇宙船で往復するとして、弟が20年経過する間に兄が16年しか経過していないといった様子を説明するやりかたである。兄から弟に送信する場合、弟は最初の16年間で兄の8年分を観測し、残りの4年間で兄の残り8年間を観測する。一方、弟から兄に送信する場合、兄ははじめの8年間で弟の4年間を観測し、残りの8年間で弟の16年間を観測する。兄と弟では、時計の進み方の切り替わるターニングポイントが違うのある。兄の場合は、方向転換した8年目がそのターニングポイントなのだが、弟の場合は、兄が方向転換した情報が伝わるのに時間がかかるので、ずっと後の16年目にターニングポイントが来る。
この、時刻信号の到着するテンポの変化は、遠ざかる音は低く、近づく音は高くなるというので知られているドップラー効果としても説明できる現象で、弟は、兄の宇宙船の信号のドップラー効果を、弟の16年目に観測し、兄は、弟を含む全宇宙の信号のドップラー効果を兄の8年目の方向転換したタイミングで観測するわけである。
この説明は、啓蒙書に多く見られるものだと、前掲書では述べられている。
3)同時線法
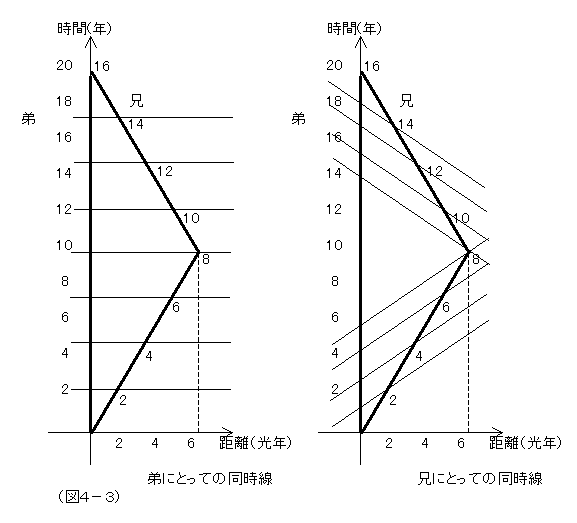
これは、弟、ないし兄のそれぞれの座標系の同時刻を表す線(空間軸)の傾きが変化していくところに注目して解説するやり方である。(この同時線は、ある座標系にとって同時だと判断される事象を結んだものであって、ある人に同時に見える事象の集まりではないことには、留意すべき。)弟の座標系では、この同時線は、常に一定の傾きを保ち、平行に推移している。しかし、兄の座標系の同時線は、地球から遠ざかる期間と、地球に近づく期間とで、傾きが異なっている。同時線の傾きが変化する時があるわけで、それは、兄が減速/加速をして、地球に向け引き返す時である。兄は、ここで大きな見かけ上の力=慣性力を感じることになる。この時、兄の座標系から判断される弟の時間の進み方は一気に早くなることになり、これが、再会時、兄よりも弟の方が年を取ってしまっている原因だと説明される。
ここで、兄の世界線を単純な折れ線で描いてしまうと、兄の一瞬の時刻に弟の数年間の経過が対応してしまい、理解に苦しむことになるが、実際は、減速/加速して方向転換するのには、ある程度の時間を要するわけで、兄の世界線は、なめらかなカーブを描き、この転換期間中に、同時刻線は、徐々に傾きを変化させていく。そしてその期間は、兄にとってはわずかな時間経過でしかないが、弟にとっては多大な時間経過に対応してしまうのである。
4)距離観測法
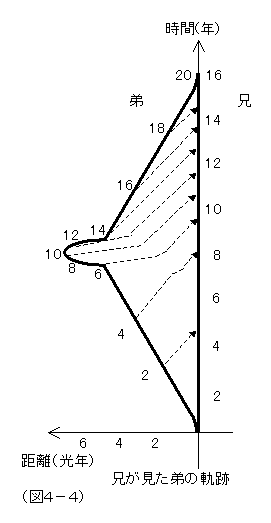
これは、弟の座標系、兄の座標系それぞれの立場から、両者の距離がどのように観測され判断されるかという点に注目して考えていくやりかたである。弟の座標系においては、運動しているのは、兄の宇宙船だけだと考えればよく、両者の距離はゼロから増加していき、兄が戻ってくるまでの期間の中間時点で、最大距離に達し、その後、縮まってゼロになるという単純な過程をたどる。弟の立場は慣性座標系であり、一様な時空なので、なにも特別に複雑なことを考える必要はない。
一方、兄の座標系ではどうか?確かに、兄から見ても、弟は始め遠ざかって行き、途中で折り返して、兄の所に近づいて来るという点では、弟の立場と全く対称的で、同等のように思えるのだが、両者の距離が具体的にどう変化するかという点にまで言及すると、対称的ではなくなる。
兄の座標系、これは、あくまでも静止しているのは兄の方だとする立場なのだが、この立場から一連の過程を解釈すると、始め、弟を乗せた地球を始めとする諸々の天体は、兄から遠ざかって行く。ここで、運動しているものの長さは縮むという相対性理論の帰結を思い起こさなくてはならない。弟の座標系では、運動するのは兄の宇宙船だけだから、兄の宇宙船の縮みだけを考えればいいことだったのだが、兄の座標系では、運動するのは、弟の乗っている宇宙全体である。従って宇宙全体の長さの縮みを考えなくてはならない。当然、兄と弟の距離も縮まっているわけで、兄から判断した両者の距離は、弟から判断した両者の距離よりも短いのである。そして、さらに、兄の座標系は一様でない。兄はあくまでも静止しつづけているわけだけれど、あるとき、突如として宇宙全体に一様な重力場が発生する。兄は、この発生をあたかも予見していたかのごとく絶妙のタイミングで、この重力によって落ちてしまわないように、ロケット噴射などで抵抗し、そのまま静止し続けるわけだが、兄の宇宙船以外のすべての宇宙の物体は、この一様重力に従って、弟からみて兄の方向に落ちて行く。もちろん遠ざかっていた弟を乗せた地球も、向きを変えて兄の方に落ちて来る。暫くすると、この宇宙全体を覆う重力場は、消えてしまう。兄の宇宙船は、その位置に静止し続けるため、やはり絶妙のタイミングで、ロケット噴射を停止させる。その後は、弟を乗せた地球その他が、慣性に従って近づいてくるのを待つのみである。
さて、この突如として発生し消滅した重力が存在している期間、兄と弟の距離について言及すると、奇妙なことが生じている。両者の相対速度は次第に小さくなって、ゼロになり、また次第に大きくなっていくという過程をたどる。ということは、速度による距離の縮みという相対論的効果が次第に減少していき、ゼロになり、また増大していくと言える。相対論的効果がゼロになったときは、弟の座標系で図った場合と同じ尺度になるわけで、これが兄から弟までの距離の最大値を示す。兄にとって、方向転換期は、このように弟との距離が急激に隔たり、また縮まるという不均質な時空を体験するときなのである。この時空においては、光は直進しない。そして、この間に弟は、ぐんと年を重ねてしまったと考えることによって、再会時に弟の方が年を取っていることを説明できる。
距離観測法は、兄の加速度座標系に則して、慣性座標系との違いに着目していく点で、一般相対論的な発想に一歩近づいている。
5)一般相対論的説明
何をもってそれが「一般相対論的」と言えるのかについては、論者によって差がある。物理の専門でない人の中には、単に、重力場がない所で、等速直線運動をしている座標系以外は、全て一般相対論の対象だと、従って、加速度運動は一般相対性理論でないと扱えないと思っている人もいるみたいだ。千代島氏もその一人のようである。しかし、大概の物理学者は、その考え方には否定的だ。単純な加速度運動は、特殊相対性理論の範囲で充分扱えるし、実際に扱っている。ただ、物理学者の間でも、対象とする時空の正味の曲率(リッチ・テンソル)がゼロでないものを扱う場合のみを、「一般相対論的」と言う人と、方法論・考え方が、時空の曲率等の一般相対論的概念に言及していくものであれば、「一般相対論的」と言っていいという人とに分かれるようだ。前者は、対象の客観的性質を基準に、後者は対象を扱う方法を基準に置いている。ここで紹介した本では、後者の立場を取ると断っている。
ただ、ここで、「特殊相対性理論の範囲で扱える」というのは、所定の問題が解けるという意味で使われているように思われる。物理学者の関心からしては、当然の視点なのだが、千代島氏のような哲学者の立場からすれば、計算問題が解けるか否かが問題なのではなく、世界観として、論理体系として、納得できるかどうかが問題になっているわけであり、加速度運動が、特殊相対性理論の範囲では充分解明できないという主張も、(千代島氏の立論から離れた一般論としてだが、)完全な誤りとも言い切れないように私には思われる。要するに、「一般相対論的」という概念は、多分に文脈依存的であることを、留意すべきであって、そこではどういう意味で使うのかを不明確にしたままだと、無用な混乱を招きやすいということは言えそうである。
さて、前置きが長くなったが、双子のパラドックスの一般相対論的説明について、述べよう。
一般に、任意の座標系において、その時空の歪み具合などを特徴付けるため、各時空点には、その近傍の時空点までの「時空距離」を定義する微分線素(の求め方)が、時空点(座標)の関数として定義されている。平坦な時空である、慣性系においては、この微分線素を求める方式は、いたるところで一定で、時間距離の二乗と空間距離の二乗の差という単純な形式(ミンコフスキー計量)である。しかし、加速度系、あるいは重力場のある系では、この微分線素の求め方は、時空内の位置によって変化していき、その表現も慣性系のような単純形ではなくなる。これが、まず、客観的に与えられた「時空の姿」の表現である。
そして、次に考えるべきことは、兄、または、弟の時空内の軌跡、即ち世界線を調べて、その線に沿った「時空距離」(=固有時間)を積分(線積分)して求めることである。
加速度系(すなわち兄が静止していると考える系)では、微分線素はやや複雑な関数になる。弟の世界線の「長さ」を計算するのには、弟が加速的に離れる時期、単調に離れる時期、加速的に弟が近づく時期、単調に近づく時期、減速的に近づく時期に場合わけして、それぞれ積分して合計を求める。この結果は、例えば、兄の世界線の8年よりも短い6年だったりすることが導け、兄の方が、ゆっくり時を刻んだことを示すことができる。
実は、最初に示した「折れ線時空図法」は、弟の座標系(=慣性座標系)のもとで、同様の固有時間の積分計算をしたことなのである。ただ、この場合、単調な座標系なので、至極簡単な計算で目的が達せられたということに過ぎない。
一般相対論的な方法に従えば、その計算の難儀さは別として、弟の立場だろうが兄の立場だろうが、どんな座標系でも、客観的に与えられたある時空内のある世界線の長さ、即ち固有時間は、確定値を持つことが示せるのであり、双子のパラドックスは、完全に解決する。
indexへ
5.千代島氏の「哲学的批判分析」
ここでは、とても、たくさんの角度から「双子のパラドックス」の論理を丁寧に分析しているようで、「双子のパラドックス」を分かりやすく、かつ「大胆」に「根源的に」解明しているようで、なによりも情熱的に書かれているので、もしかすると、読む人によっては、退屈だとは思わないで、至極感銘を受けるのかもしれない。とは言っても、私ごときものですら、いささか首を傾げてしまいたくなる所が随所に散見される内容でもある。いわゆる、相対性理論をあからさまに否定する系の立場を明言しきってもいないので、分かりづらくはあるのだが。もちろん、物理学の専門家などよく分かっている人にとっては、失笑するのみで、わざわざとりたててどうこうなんて気にもならないのかもしれない。ただ、私は、ここには、物理学を日常的言語の世界に引き入れて、「分かりやすく」解釈したいと思う者(私自信も含めて)が、概して陥りやすい、注意すべき陥穽が典型的に現れているようで、少し言及してみたくなったのである。
第1章 序論 - パラドックスの本質は何か
第1章では、先ず、パラドックスの何たるかの説明がなされる。「双子のパラドックス」を解くための最重要課題は、「はたして加速度運動は相対的か」という問いに答えることだとされる。つまり、兄が加速度運動をしているとも、弟が加速度運動しているとも対称的に言えるのじゃないか、それなのに兄の方だけが時間の進みが遅くなるのは、矛盾であって、これが矛盾でないことをいかに示すかが、課題なのである。なるほど。
第2章 ニュートンに立ち返って根源的に考え直す
だが、その前提として、まず、ニュートンに立ち返るところから始めて、相対性理論が何故、時間の遅れのようなことを言うようになったのかを根源的に問い直さねばならないということで、第2章で、ニュートンやライプニッツの考え方について言及される。ニュートンの絶対時間や絶対空間の考え方では、時間の遅れはありえず、パラドックスも起き得ないわけだが、ニュートンの考え方は、欠陥があって、今日受け入れられえないという、周知の事実に対して、これをアインシュタインの考え方に頼って克服するのは、「紋切り型の批判」で退屈なのだそうだ。(私などは、退屈かどうかということよりも科学史としてどうなのかの方が、重要なのではと、安直に思ってしまうのだが。)
そこで、登場するのは、同時代のニュートン最大のライバル、ライプニッツである。ライプニッツは、空間を物と物とが同時に存在する関係・秩序、時間を出来事間の関係・秩序という見方をし、実在する諸物体、諸事件から独立して存在する、空虚な時間、空間という固定的な容れ物のようなものを想定していたニュートンとは異なる時間、空間に対する観念を主張していた。千代島氏はこの点をとりあげ、ライプニッツはアインシュタインを先取りしていたと評す。この章では、ニュートンの側に立つクラークとライプニッツとの論争を紹介しながら、ライプニッツを持ち上げている。ここでの展開は、哲学史に興味のある人にとって、いくばくかの「退屈」さの克服になったのかもしれないが、「双子のパラドックス」の問題に向き合う上で、この展開にどれだけの必然性があることなのか、私には、どうも理解できなかった。
第3章 特殊相対性理論における時間の本質
第3章から、やっと相対性理論の解説に入る。まず、実験や計算だけに頼る物理学者の姿勢は、なんら難問を解決することに至らないと、こっぴどく批判されるところから入る。哲学者・千代島氏の得意とするところのようである。私は、物理学者ではないから、よく分からないのだが、発見的過程で試行的に色々計算してみるということは、物理学者じゃなくても色々な分野でよくやられていることだけれど、一応、確定した理論的説明をする段階においては、普通、どんな物理学者でも、その背景となる物理的イメージを理解した上で、その具体的で厳密な解を求める目的で計算をしているんじゃないかと私などは思ってしまうのだが、千代島氏の周りの物理学者はそうではないのだろうか。
扱う対象が、複雑で、巨大な計算業務を、プロジェクトを組んで行うような場合、個々のメンバーが担当する計算の物理的意味をいちいち考えている余裕も意味もないというような場合はあるのかもしれないけれど。また、量子物理を応用した研究現場で、いちいちシュレーディンガーの猫のことなど考えていられないということなら、まあわかるけど、「双子のパラドックス」の説明をするというシチュエーションで、計算だけですまされたと取られたのは、たぶん、物理学者にとっては当然の了解事項を端折って説明してしまったからとかの、言葉足らずが原因ではないだろうか、と想像する。その人本人自身が何の物理的イメージも持たないで、計算だけしてみせるというのは、それはそれですごく不思議なことだ。(ありがちなのだろうか?)まあ少なくとも、千代島氏を充分納得させられるくらいに親切丁寧な物理学者に千代島氏が出会うことがなかったということは言えるのかもしれない。
それは、それとして、ここでは、千代島氏による相対性理論の概説が展開される。アインシュタインは、速さ一定の光によって時間を定義したというところの革命性がまず解説される。それによって、同時刻が相対的になってしまうこと、光の速さが常に一定であるためには、慣性系は互いにどのような数学的関係によって結ばれるべきかということでローレンツ変換が導かれ、それによれば、時間の遅れや長さの収縮が導かれることが、説明される。細かいことは別として、オーソドックスな説明である。
ユニークなのはニュートンは「神の立場」で、ライプニッツやアインシュタインは主に「人間の立場」とするくだりだろうか。ここでは、絶対的な観点を「神の立場」、相対的な観点を「人間の立場」と表現しているようだ。このようなもったいぶった表現を採用するとすれば、私は、物理学者(自然科学者)は、昔も今も基本的には「神の立場」だと思う。ただ、より完成度の高い「神の立場」は、すべての「人間の立場」を平等に扱える。アインシュタインは、そのような方向性で「神の立場」の完成度を高めたのだ。絶対性の観点があるからこそ、すべての相対性が扱えるのである。アインシュタインは、絶対的で普遍的なものの何たるかについての視点を変革することによって、すべての相対的な観点を矛盾のない体系に高めることに成功した。その結果、今まで、絶対的と思われていたものが、相対的なものになってしまい、彼の理論は「相対性理論」と呼ばれるようになった。(彼が自分の理論を「相対性理論」と呼ばれることをあまり快く思ってなかったというのは、有名なエピソードである。)ここで言う「神の立場」と「人間の立場」は、内包的関係にあるのであって、対立的な関係にあるのではない、という風に捉えるべきだと私は思っている。
哲学者・千代島氏は、単純に相対性理論を説明してすますことはしない。随所で、哲学的批判分析を加えることを怠らない。そして、安易にアインシュタインの権威にすがって批判的考察をしない物理学者たちを叱咤激励している。例えば、こんな風に。
はたして我々は、現代において本気で物理学者たちを尊敬できるであろうか?
否、否、三度否である!自分の業績とは何の関係もない過去の偉大な英雄たちの栄光にしがみつき、必死でそれを守り抜くことに汲々としているようでは、物理学が沈滞してしまうのは当然である。(p149)
(なお、このくだりは、新版「双子のパラドックスの論理」では割愛されている。)
いやはや、三度も否と言われてしまっては、物理学者も立つ瀬がなかろう。しかし、千代島氏の哲学的批判の論点は、意外に単純なところに集約されそうだ。曰く、「それは、循環論法ではないか!」と。
例えば、相対性理論の基礎における論理的循環として、次のような指摘がなされる。
相対性理論は、「速さが一定の光」によって、「時間」を定義している。一方、その「時間」を使って、「距離/時間」として、「速さ」を定義している。これは、明らかに、論理的循環である。
ちなみに、相対性理論では、「速さ」の概念を、ニュートン力学のままで理解してはならない。「距離/時間」という定義では、どの座標系の距離や時間なのかを言わなくてはならないからやっかいである。むしろ、光速に対する比として、速度という概念は再定義されていると考えたほうがシンプルである。速度の加減算も再定義されている。一定の極限値である光速を基準にした形で、距離や時間の概念と共に、速さの概念も再編成された一連の論理モデルが全体として形成されているのだ。その点を踏まえた上で、上記の指摘は何がしかの意味を持ちえるのか、考えてみるべきであろう。
第4章 一般相対性理論における運動の本質
第4章は、一般相対性理論についてである。先ほどでも、触れたが、千代島氏の特殊相対性理論と、一般相対性理論との線引きは、加速度運動を扱うか否かのところで引かれているので、一般の物理学者の考え方とは違う。時空の歪み等の概念はここでは全然登場しないので、一般の物理学者の考えている一般相対性理論については、殆ど触れられていないと言った方がいいかもしれない。重力についても、一方向でのことしか語られないので、慣性力か重力かといった、加速度系ないし重力系のごく単純な側面のみが扱われている。テーマは、「双子のパラドックス」をめぐってのことなので、これでもいいのかもしれない。
ここでは、おなじみのエレベータの落下の問題が出てくる。ここで、アインシュタインは、エレベータの中の立場でもなく、エレベータの外の立場でもない第三の立場、「観測者の観測者」という「神の立場」から眺めているのだということが強調される。そういう立場に立つということが、何故、特殊相対性理論ではなく、一般相対性理論特有のことなのか理解できなかった。特殊相対論だって、どの座標系にも属さない、すべての観測者を観測する視点は持ち合わせていると思うのだが。
第5章 二種類の運動と「矛盾」の関係を論理的に明確化する
第5章では、そもそも矛盾が矛盾と言える条件は何であるか、ということが展開される。一番、論理学者らしい展開の部分とでも言っておこうか。
あれこれの説明の後、明示されたことは、
矛盾が生じるのは、
(1) 同じものについて
(2) 相反する主張が
(3) 同じ観点(立場)から
(4) 同時に
なされる場合
であることである。
それで、等速直線運動している兄と弟の間で、互いに相手の時計の遅れを主張しあうことは、兄と弟が「異なる座標系」にいるから、これは、日本とブラジルの住人が、同時に今は昼だ、夜だと言い合っても矛盾でないのと同様、これは矛盾ではないと、説かれる。
しかし、加速度運動する兄が加速度運動しない弟のところに戻って来て再会するような場合は、正真正銘の矛盾なのである。なぜなら、両者は「同じ座標系」に静止しているから、すなわち「同一の観点(立場)」から観測しているから、ということらしい。
ちなみに、「双子のパラドックス」の場合、両者が再会する瞬間、両者は互いに静止していることは要請されていない。すれ違う瞬時の互いの観測で、互いに相手の時計が、遅れていると言い合う事態が起きればそれは、矛盾だ。相対性理論によれば、実際はそうではなく、兄の方が遅れている事実を両者がともにこの瞬間認知するのである。さて、この場合、両者は静止していない。「異なる座標系」にいる。千代島氏の説によれば、静止しないですれ違う場合は、兄と弟の見解が異なっても矛盾でないことになってしまい、本来の「双子のパラドックス」より甘い基準になってしまう。
相対性理論の場合、同時かつ同地点の事象についての観測は、いかなる座標系においても、一致しないといけない。そうでなければ、物理学体系として矛盾であり、理論として成立しない。ただ、離れた場所の出来事が同時か否かは、座標系に依存するのである。そして、時間の進み具合も、地点間の距離も座標系に依存するのである。しかし、同時かつ同地点のものについての見解は一致していないといけない。兄と弟が離れているときは、それぞれの相手に対する見解が異なってもかまわないのだが、再会した瞬間は見解は一致していないといけないのである。「双子のパラドックス」は、この原則がどのようにして守られるかの仕組みを説明する問題なのである。
互いに等速直線運動している兄と弟の場合、同時かつ同地点になる機会は一度しかない。これは時計を互いにリセットする瞬間だ。この先、両者の時計を付き合わせる機会は訪れない。それぞれがそれぞれの基準に従って、相手を評価するしかない。その場合、例よって「神の立場」から言えば、両者は互いに相手の時計が遅れているはずだと主張しあうことになるのである。これは、同時かつ同地点での主張ではないので、矛盾ではないのである。
「双子のパラドックス」の問題を考える上で、矛盾か否かを判断する基準は、「同時かつ同地点」ということなのである。千代島氏の述べるように、「同一の観点(立場)」「同じ座標系」という基準で判断しては、問題が曖昧な形で、はぐらかされてしまう。
もっとも、他の部分の叙述を読むと、両者が再会する時に互いに静止している必要がないことは、千代島氏も理解しているようにも取れるのだが、そうだとすると、ここで述べたことは、単なる言い間違いなのだろうか。だとすると、この章の展開は何なのだろう。不思議が多いこの一冊。
第6章 特殊相対性理論ではパラドックスを解決できない
さて、準備段階も終えていよいよ本題に入る。ここでの各節の表題をとりあえず以下に列挙しておこう。
1 ローレンツ変換を用いる計算?
2 ミンコフスキー・ダイヤグラム
3 同時刻を表す直線
4 結論を先取りする証明(循環論法)は無意味
5 奇妙な時間の飛躍と「乗り換え」理論で欠点が露呈する
6 「三人兄弟」の理論も本質は同じ
7 ロケットの立場から考えた理想的な理論も失敗する
8 ドップラー効果を利用する理論
9 「みかけの力」の非対称性に訴えても解決できない
10 最も素朴な三角不等式の理論
双子のパラドックスの解明法を、ずいぶん熱心に集めたものだと感心してしまう。しかし、読んで行くと、細かなところで突っ込みを入れたくなってしまうのだが(※1)、本稿の読者をこれ以上、退屈にさせるわけにはいかないと思うのでやめる。本質的な議論に絞ることにしよう。
千代島氏は、これでもかと言わんばかりに、数々の双子のパラドックスの解法を取り上げては、指摘し続けていることは、ただ、次の一点に集約される。
これらの理論は、どれも皆、ロケットに乗った兄の側が加速度運動していることを前提にしている。我々が真に証明しなくてはならないことは、なぜ、弟の方が加速度運動しているのではなくて、兄の方が加速度運動しているかを示すことであるはずなのに、これでは、結論を先取りした循環論法であって、何も問題を解決したことにはなっていないのである、と。
実際のところどうなのか。別に兄が静止し、弟が加速度運動しているという見方を相対性理論は否定してはいないという意味では、表現上間違った指摘だと言うこともできるかもしれないが、弟の立場と兄の立場の非対称性、兄の側が特別に加速度運動をする、もしくは、あるとき、急に一様重力場に飲み込まれるという点で、弟の終始、一様にあり続ける立場とは違っていることを、はなから前提して議論しているということは、間違った指摘ではないと、私は思っている。そう、兄の側が特別なのだということを前提しているというこの主張は正しい。だが、そもそも、こんなことを指摘すること自体に、根源的な無理解と混乱がある。
物理学者は、兄と弟の立場の非対称性を(対称的かどうかわからないところから)証明しようなんて、微塵も思っていないのである。これは、一つの事例として掲げられた前提なのだ。だから分かりきったことなのだ。物理学者がやろうとしていることは、この前提の成立つ場合においては、どのように、兄の側の時計の進みが弟のそれより遅れることになるに至るのかの仕組みを説明しようとしているのである。
だが、千代島氏は、この一事例としての前提が証明もされないで前提されてしまっていることをもって、物理学者は双子のパラドックスを真に解決していないと主張する。
(※1) ちょっと気になるところをかいつまんで述べよう。
・「2 ミンコフスキー・ダイヤグラム」で、ミンコフスキー四次元時空は、「発見」ではなく、発明だと述べられている(p213)。私は逆に、「発見」だと考えている。これについては、「双子のパラドックス」の主題とはずれる問題なのだが、本質的な事柄でもあるので、第8章で、別途議論を展開したい。
・「4 結論を先取りする証明(循環論法)は無意味」(p222)(新版p137)において、(1) まず、地球の弟の座標系を基準としてローレンツ変換で計算すると、運動した兄の時計が遅れることが示される。とあるが、(2)の方は、意味が不明。普通、弟の時計が遅れることが示されることになるはず。ローレンツ変換がどのように適用されたことを述べているのだろうか?というより、「ローレンツ変換で計算する」というその計算がここで具体的に何をさしているのか意味不明。
(2) 次にロケットの兄の座標系を基準としてローレンツ変換で計算すると、兄の時計が遅れることが示される。
・「5 奇妙な時間の飛躍と「乗り換え」理論で欠点が露呈する」において、同時刻を表す空間軸が折り返し時点で傾きを変えてしまうことによる「突然の時間の飛躍」が奇怪だと述べられるが、実際は、連続的な変化であることの簡略表現だということを理解していないのだろうか?それともゼノンのごとく、変化そのものが飛躍なりという根源的な言明をしているのだろうか。だとすればこれは、「無限」や「連続性」の問題とかになって、本テーマとずれてしまう。
・「8 ドップラー効果を利用する理論」のところで、兄が静止しているとみなす場合の図が書いてあるが(p253)(新版p159)、この場合、光は必ずしも直進しないし、弟の世界線は、折り返し点付近で、急激に兄から離れる形になることを理解していないのだろうか。(本稿、「4.-4)距離観測法」参照。)なお、この図の問題はこのページに限った話ではないが。とにかく、兄が静止し、弟(と全宇宙)が加速度運動する場合の時空図は、弟が(全宇宙と共に)静止し、兄が加速度運動する場合の時空図と対称的にはならないのである。
・「9 「みかけの力」の非対称性に訴えても解決できない」での議論も、相変わらず、結論を先取りした循環論法だという批判で片付けられているが、私は、別の意味で、「みかけの力」の非対称性に訴えるやり方は、しかるべき前提条件を明示しないと、不用意な誤解に導く危険性があると思っている。これは次章で説明する。
(※本文に戻る)
1)第7章 パラドックスを解決する手掛かりを求める
そして、この章で、「双子のパラドックスの真の解決は、 加速度運動は相対的ではない ということを明確に説明することによってのみなされるのである」と述べられる。その手掛かりは、もし、地球が加速度運動するのなら、その原因として、「大きな物体の重力の作用」を想定しなくてはならないということだと推定される。さらに、また、ライプニッツの抽象的な命題を引き合いに出しながら、これまでの議論が地球とロケットという「二つ」の対象の関係しか考えてこなかったことに、ここにいたって漸く気付くに至るのである。
1)第8章 結論 - パラドックスの最終的解決
そして、最終章で、パラドックスの最終的解決が述べられるわけだ。
千代島氏は、双子のパラドックスでは、「宇宙には地球とロケットしか存在しない」かのような前提がなされていたのだと、指摘する。そう思っていたのは、千代島氏だけではないのか?物理学者がそんな前提で双子のパラドックスを論じていたとは私には思えないのだが。だが、物理学者が、関心を注ぐのは、どのような仕組で、兄の側の時間が遅れるのかについて叙述することの方にあって、弟のいる地球系は、単独のものではなく、言わばその近傍の宇宙系の代表として掲げられているということを、いちいち丁寧に明示的に述べたりしない場合が多いのかもしれない。それで、物理学者たちはここでまた、叱咤激励されることになるのである。「抽象的で機械的な思考から抜け出さねばならない。そして、具体的で、総合的な、根源的考察をするように心がけねばならない。」と。
そして、待ちに待った最終結論は、こうだ。ロケットの兄が静止して地球が加速度運動するという立場では、地球以外の多くの星々もまた同様の加速度運動をしていると見なさなくてはならず、この点で、対称性が崩れる。つまり矛盾(パラドックス)の成立条件がなくなる。そして、もし、地球や他の星々が一斉に加速度運動を行うには、宇宙のかなたに超巨大な物体が重力作用を及ぼさなくてはならないはずだが、そんなことはナンセンスだ。だから、加速度運動しているのは、ロケットの兄の方なのである、と。
ここに至り、読者は、唖然としてしまうことになる。双子のパラドックスの問題を通して、明らかにしたかったことは、このように一方が単独に加速度運動をして再会する場合、時間の進みがどうなるのか、そして、それは何故、どのような理由でそうなるのか、さらに踏み込んで、どの程度のずれが生じると計算できるのか、というようなことなのだ。そして、それを具体的に説明したものが、第6章で、千代島氏が紹介した数々の論証なのである。ところが、千代島氏によれば、このケースにおいてはと最初に仮定されていた分かりきった前提条件をあえて証明することこそが、双子のパラドックス解決の真髄なのだと理解されてしまっている。そして、本来は主眼たるべき論証部分がそれこそ抽象的な「循環論法」論法によって、ことごとく一蹴されてしまうのである。
千代島氏のこの混乱の原因は、一つには、一般相対性理論がとても浅くしか理解されていないことによるものかと思われる。何故なら、兄が静止し、弟が加速度運動をするという時空図(世界線)は、弟が静止し、兄が加速度運動をするという時空図(世界線)と、全く対称的な図になると信じているからだ。前者は、弟と地球その他の天体が兄に向かって折り返す時に、時空が歪んでしまい兄と弟間の距離が引き伸ばされ、光速も一定でなくなるということが、分かっていれば、こんな議論は提起しなかったのではと思う。なお、ついでに付け加えておくと、弟(を含む宇宙)側が加速度運動するというようなこの一様重力場においては、超巨大な物体を別に想定しなくてもよい。一般相対性理論が、大きな質量(エネルギー)の集中を要請するのは、場所によって重力の大きさや方向が異なるような重力場が存在する場合である。
さらに、つきつめて考えてみたのだが、千代島氏は、物理理論を、素朴な命題論理の連結体系のようにしか捉えていないのではないかというところにも、混乱の一因があるのではないかとも、私は思うのである。この点については、第7章で、触れてみたい。
ともあれ、千代島氏にとって、一方が加速度運動をしているということが、最初から前提されてしまった議論は、納得がいかないらしいことは、はっきりしている。では、これを前提にしないで、「双子のパラドックス」の問題を考えたら、どうなるのか、次の章ではそういう視点で、このテーマを考えてみよう。
indexへ
6.二人は離れ、そして再会する - その場合分け
双子の兄は宇宙船に乗り、弟は地球に留まる。そもそも、この設定が両者の立場を対等にしていない。だったら、兄も弟も共に別々の宇宙船に乗ってもらう。そして、出発点、すなわち、兄と弟が同時に同じ地点で接して、最初の時計合わせをするところは、付近に地球などの天体がない、空漠とした宇宙のある時空点だとしよう。この時、両者は必ずしも互いに静止している、すなわち同じ慣性座標系にいる必要はない。
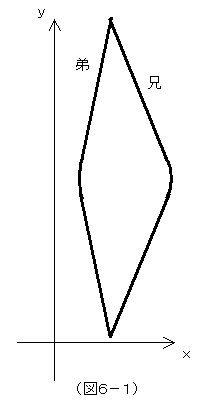
そして、宇宙のある時空点で接した兄と弟は、互いに別々の方向に飛び去っていくとする。両者が任意の方向に飛び去り任意の飛行をして、再び出会う確率は、絶望的に少ない。何がしかの計画を立てるか、何らかの連絡を取り合うかなどして、互いに制御した飛行をしない限り、両者が再び会うことは望めないだろう。そして両者が再会しない限り、パラドックスの要である時計の見比べはできないのだから、とにかく両者は、その後、再会するような飛行をするということは、前提しよう。だが、前提はここまでとする。(図6-1)
さて、再会した兄と弟、どちらが若い状態だろうか。つまり、より少ない時間を経過した(時計の進みが遅くなった)のはどちらだろうか。それともどちらも同じだけの時間経過が与えられて、差はないのだろうか?
この場合、答えは「どちらとも言えない」である。それぞれが、宇宙の中のどういうコースをどのように飛行したかによって、結果は違ってくる。つまり、場合分けをして考えなければならない。
では、どんな場合分けをすればよいのだろうか。つまり、場合分けの基準を何にすればよいのだろうか。
まず、強力な、慣性力(加速度系に生じる見かけ上の力、あえて重力と呼んでもいいが)を体験するかどうかを基準にするということが考えられる。これは、宇宙船に乗る者が、窓の外を観測し続けていなくても感知できる事実根拠となりえて、とても指標にしやすい。
その場合、強力な「慣性力」を
(1)兄が弟より強力に体験
(2)弟が兄より強力に体験
(3)双方が同じくらいに体験
と場合分けして、(ここで「強力に」という表現は強さとそれがかかった延べの時間の双方が加味されたものと理解してほしい)
これに対応させて、
(1)は、兄の時間の進みの方が遅い
(2)は、弟の時間の進みの方が遅い
(3)は、双方の時間の進みは等しい
と言って良いだろうか。
一見、良さそうだが、答えは「ノー」である。これが、言えるためには、次のことが前提されなくてはならない。
両者は、一様な重力場、たとえば、物質・エネルギーがほぼ均等に分布しているような時空において飛行し、その飛行方向は、基本的には一つの真直ぐな空間軸に沿ったものであること。
どういうことかと言うと、宇宙船が行って引き返すという飛行は、ロケット噴射などに頼らず、ある天体の重力場を利用することもできるわけだが、(こちらの方が断然エネルギー的にお値打ちだが、)この場合、宇宙船に乗った者は、何も慣性力は感じないで(無重力状態のままで)折り返しが出来る。弟から遠く離れた兄はこうして折り返し飛行をするとしよう。一方、弟は、ある場所(ある慣性系の一地点)を中心に行ったり来たりの往復を繰り返すとか、回転運動をしているとかしながら飛行してたとしよう。すると、弟は兄よりも、慣性力(遠心力もその一つ)を強く体験することになる。そして、再会した場合、結果はどうか? 慣性力を体験していない兄の方が体験した弟より若い、時間の刻み方が兄の方が遅いのだ。上に掲げた仮説とは逆の結果になる。ロケット噴射で慣性力を体験して引き返そうが、天体の引力を利用して無重力感のまま引き返そうが、やはり弟から遠く離れて引き返した兄の方が、時間の進み方が遅くなる。(図6-2)
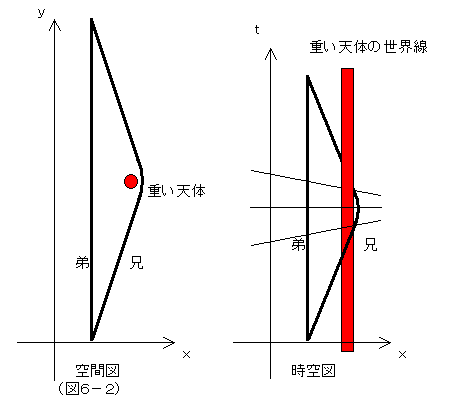
だが、今度は、弟の方も宇宙船に乗って飛行しているのだ。地球やその他の星々に対して、静止しているわけではない。とすれば、兄が静止しているとみなす座標系に従えば、弟の方こそ、加速度運動していると言っていいのではないか?であれば、弟の方が時間が遅れると言えるのではないか?まさにパラドックスではないのか?
いや、そうではない。兄は静止し続けているという観点を守るとしよう。ある時、兄にある天体が近づいてきた。この時、弟を含む宇宙が、兄に向かって急に運動方向を変えて、兄に向かい始めたのである。兄は何も慣性力を感じていないのだし、自分が加速度運動をしたとは思いたくないとしよう。とすれば、この天体が近づいてきたところで、時空全体が歪んでしまい、それで、弟の宇宙船は、その他諸々の物と同様に方向転換をしたのだ、と解釈することになる。この方向転換期では、弟との距離が急激に増えたり減ったりするわけで、構造的には、兄の宇宙船の推進力を使った場合と同様の経過になるのである。
では、兄と同様に、弟も大きな天体に遭遇した場合を考えてみよう。ここで、弟は、その天体に引き寄せられて方向転換をしてしまわないように、ロケット噴射をして、進行方向の保持に努めたとしよう。すると、弟は「慣性力」を感じる。(ニュートン力学では、これこそが、「重力」と呼ばれるべき力だ。)つまり、時空の測地線に沿わない世界線を弟は辿ったわけで、それで慣性力ないし重力を感じることになる。一方、兄は、時空の歪みに抵抗することなく飛行して引き返してきたわけで、その結果両者は再会したとしよう。結果はどうか?慣性力を大いに体験した弟の方がそうでない兄よりも時間の経過は遅いかと言えば、そうではなく、やはり、兄の方が時間の経過が遅いのである。(図6-3)
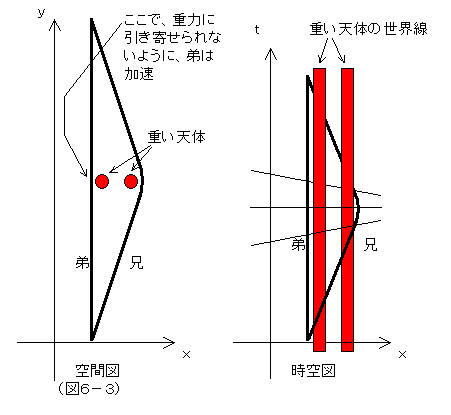
あるいはまた、兄は、体感的には、地球の重力場のもとで暮らすのと全く同じ状態で宇宙旅行することも出来る。1G(≒9.8m/sec2)で、一方向に1年(地球時間)も連続して加速しつづければ、光速の77%、3年で、光速の99.5%に達する。(技術的、エネルギー経済的に難しいけれど。)方向転換時には、1Gの遠心力がかかるようにUターンし、帰りは後ろ向きに1Gで減速すれば、旅行中はずっと1Gで暮らし続けられる。もちろん、再会時の結果は兄のほうが若い。
つまり、先に掲げた理想化された前提を抜きにすると、「慣性力」をどのように体験したかは、時間の遅れについての決定的な要因にはなんらなり得ないのである。だから、もし、前章で紹介した千代島氏の「周りの星々を見よ云々」の主張を批判しようとして、「慣性力」が観測されたかどうかが、兄と弟との差異、非対称性を決定づける最大の根拠だというような言い方をしたとすると、別な意味で誤解と混乱に導く可能性が出てきて危ういと思う。これでは、非対称性を証明することこそが肝要なのだという千代島氏の誤謬に引き込まれてしまっている。
それで、「慣性力」の体験は指標にならないとすれば、どんな具合に場合分けを考えていけばよいのだろう。
考え方の方針として、次のように進めたらどうだろうか。まず、兄と弟が再会できて、なお、時間の進み方について双方に何の差もないことになる条件は何か、を考える。そうすれば、その条件からのずれが、いずれかの時間の刻みが遅れることになる条件だと考えて行けるのではないだろうか。
再会するには、片方もしくは双方の「方向転換」が必要である。それには、ロケットエンジンなどを噴かして、自ら加速(減速)をするというやり方と、天体の重力を利用するというやりかたがある。
それで、兄と弟は互いに相手の方に、同じだけ、加速して方向転換を図る、もしくは同じだけ重力の影響を受けて方向転換を図る。こうして再会したら、両者に時間経過の差異は生じないはず。だから、これを基準にして、どちらがより強力に加速をしたか、あるいは重力の影響を受けたかで、時間経過の遅れがどちらにあるかを判断できるのではないか。
一見よさそうだが、実はそう単純ではない。方向転換するタイミング等も重要である。もし、兄が弟より早めに方向転換して弟に近づいて行ける速度で引き返したとする。遅れて弟は同じだけの加速で方向転換して兄に近づくとすると、そこから再会するまでの時間は、兄が出発してから方向転換するまでの時間よりもずっと短い。「同時線法」で考えると分かりやすいと思うが、兄が方向転換した時、弟との距離は充分離れていて、弟の時間が急激に経過してしまう度合いが大きい。これに比して弟が方向転換する時は、兄との距離は充分になくて、兄の時間が急激に経過してしまう度合いは少ない。従って、再会した時は、兄の時間経過の方が少ないという結果になる。方向転換時において、相手とどれだけ距離を隔てているか、という点も、重要なファクターなのである。相対論的効果を大きくするには、もし、両者が近い距離にいたなら、かなり強烈な加速が必要だが、遠く離れていたなら、少ない加速でも、充分に効果を出せてしまうのである。従って、「時間の進み方について双方に何の差もないことになる条件」としては、方向転換時における相手との距離が同等となるように、方向転換するタイミングも等しくするとか、方向転換しても、先に相手に近づいては行かないなどの考慮をしなくてはならない、ということになる。
以上の考察で、時間の遅れをもたらす系かどうかの判断基準として、以下の二つを抽出できたわけだ。
(1)自らの加減速、または重力の影響による、方向転換の度合い
(2)方向転換時における、相手との距離
これらに基づいて考えれば、兄と弟、どちらの時間進行に遅れが生じるかについて、おおよそ、場合分けが可能になるだろう。
ただし、以上の考察は、一般相対論特有の効果を無視できる程度の加速、または重力場においてということを暗黙に前提している。
先程、慣性力をどれだけ強く体験したかは、時間進行の遅れに、直結しているわけではないことを述べたが、これも度を越した場合はさにあらず、ということになる。極端に強い重力場(時空の歪み)にはまれば、それ自体で、時間進行の遅れをもたらす。この顕著な例は、ブラックホールに落ち込んでいく物体の時間進行は、ブラックホールから隔たった系で判断すると、永遠に止まってしまうということなどである。だが、この効果を体感できるほどに顕著にさせることができるような加速系、重力系は、ぺしゃんこに潰れたり、引き千切れてしまったりと、人間の生身には過酷すぎるだろう。
以上の議論、所詮は定性的な、つまり厳密性に欠けた議論である。場合分けという考え方は、ある条件の効果をはっきりさせるために、別の条件を理想化・単純化させたりといったことをせざるをえないだろうから、一般的な複合的状況については語れない。本当に、完全に一般的に、かつ定量的に判定していこうとするなら、千代島氏が軽蔑してやまない(私の場合は、尊敬するのだが、能力的についていけない)いわゆる数式を立てて計算するという手法が、不可欠となるだろう。
先ず、しなければならないことは、所与の時空の計量構造が、全体としてどうなっているのか、そのモデルを築くことである。次に、兄と弟、それぞれがどのような世界線として、その時空内に存在することになるのかを求める。その世界線が、その時空内での測地線からずれていれば、そこで「慣性力」が感知されるだろう。以上の情報収集作業ができたら、それぞれの世界線の線積分を計算する。これが、それぞれの世界線の「固有時間」(そのコースを辿った者が体験する経過時間)を表している。ここでの線積分とは、世界線を微小な要素に分割して、その短い世界線が静止しているとみなせるような座標系で測った線分の長さ(時間を表す)の総和を求めることである。線積分の計算根拠となる線素(の求め方)は、所与の時空座標の関数であり、その場での質量(エネルギー)密度の分布に依存する。平坦な時空では、その線素は、ミンコフスキー計量で表されるし、重力場のある歪んだ時空では、より複雑なテンソル表現が必要になる。なお、全体としての所与の時空をどのような座標系(兄の立場か、弟の立場か、別の第三者の立場か)で表現するかは、任意である。どんな立場からしても、それぞれの世界線の線積分した値(各人の固有時間)に違いはない。かくして計算された兄と弟の固有時間を比較して、その値が小さければ、時間経過が少ない、つまり、出会った時、より若い、と判断できる。
とにかく、どんな時空内で、どんな飛行をするかという情報収集こそが、重要なのである。この情報収集は、言い換えれば、「観測」である。これには、千代島氏が最後に強調していた、「地球以外の多くの星々が地球と同様の加速度運動しているかどうか」といったことを確かめる観測ももちろん含まれる。ただ、窓から見える景色の観測だけでは、不確かな場合もあるから、「慣性力」があったかどうか、それは回転によるものでないかどうかを判断するためのコリオリ力のチェックなど、あれこれ注意深く観測して、多くの情報を集めて総合的に判定しないと、客観的なモデルの把握に失敗する可能性がある。場合によっては、宇宙の9割以上を占めていると言われている謎の暗黒物質、暗黒エネルギーの存在も考慮しないといけないかもしれない。
宇宙は、様々な天体やエネルギーが様々な方向に運動していて、複雑であり、その中において、任意のコースを辿って再会する双子の固有時間を厳密に計算して求めることは、一般には、たいへん難しい。
以上のような、ややこしい話を、相対性理論の入門書レベルで、ごたごた述べるわけにはおそらくいかないだろう。それで、一番身近で、シンプルな事例として、弟は地球に残り、兄は宇宙船に乗って遠くに行って、戻ってくるというパターンが、選ばれたのである。だから、この場合は、どんな時空内で、どんな飛行をするかという情報収集作業は必要ないわけで、既知の事実として、前提すればよいわけだ。そこのところを千代島氏は勘違いしたため、奇妙な論理展開の前掲書が生まれるに至ったわけである。
indexへ
7.物理理論の中の循環論法について
先に見てきたように、千代島氏は、物理学者による「双子のパラドックス」の説明は、皆、ことごとく結論を先取りした循環論法だ、という批判をする。これについて、私は、ある場合についての説明としての前提にすぎないということに気付かないで、勘違いしているのではないか、と指摘した。
ただ、単なる勘違いで片付けられるべきでないもっと根深い問題を私は感じている。千代島氏は、物理学の理論を論理学的に分析して、その結果、これは、循環論法ではないかという批判に至ったわけなのだが、双子のパラドックスに限らず、一般に物理理論には、一見、循環論法ではないか思わせるような様相が、あるものなのではないだろうか。
物理理論は、それ自体、ある閉じた論理体系になっており、ある事柄は、別の事柄を論理的に導くと同時に、その別の事柄が巡り巡って最初の事柄を証明することにもなりうる。ある命題から別の命題へと証明が一通りのやり方でつながっている姿だけがあるわけではない。互いに支えあった命題群の集まりと見るべきだろう。要は、措定されているのは、特定の原理命題なのではなく、数理論理モデル全体が措定されていると考えるべきなのだ。
ある論理モデルにおいて、どの命題を公理に置き、どの命題を定理に位置付けるかは、任意に置換え可能である。例えば、ユークリッド幾何学の平行線の公理の代わりに、三平方の定理を公理に置いて、平行線の公理を定理として導く形にすることも可能である。どちらを公理に置いても、両者は、同等の、ユークリッド幾何学の論理モデルになっている。そして、両者は、平行線の公理命題、あるいは、三平方の「公理」命題を否定ないし別物に変えた、幾何学体系(曲面/曲空間幾何(リーマン幾何学))とは、一線を画した特定の論理モデルになっているのである。
重要なことはどのような種類の論理モデルが適用されるか、であり、個々の命題のどれを公理(原理)に選択するかは、その論理モデルの表現上の問題でしかない。通常は、分かりやすさ、簡潔さ、扱いやすさが考慮されて、公理命題は選ばれる。特殊相対論では、光速不変原理と相対性原理が、原理命題として、位置付けられ構成されているが、光速不変原理の代わりに定理である同時刻の相対性や、ローレンツ変換、ミンコフスキー計量などを公理に置き換えても、同等の論理モデルが成立するはずである。あるいは群論のような抽象代数学的論理モデルからアプローチすることも可能であろう。それらはしかし、表現上の違いであって、同等の物理的内容を表現した論理モデルである。科学は、一連の現象を、総合的に矛盾なく説明するためにどのような論理モデルが妥当かを考え、それを仮説として提示し、検証を繰返して、確たるものに仕上げていく。物理学の場合、この論理モデルは、数学的なモデルが適用されるので、厳密である。そして、この論理モデルの実際の検証プロセスには、モデルの具体化が不可欠である。一般論として提示されている論理モデルは、抽象的なものなので、検証例に基づいて、具体化しなくはならない。つまり、それぞれの事例に合わせて条件設定をしなくてはならない。そうして、具体的な観測結果との照合を行う。全ての事例を検証するのは、原理的に不可能なのだから、この照合が、必要にして十分と判断できる程度のケースにわたって成功すれば、この論理モデルは、さし当たって、正しいものと認定されるわけだ。
こういった論理モデルの枠内で展開されているものを、部分的に切り出してあげつらうと、今回示したように場合によっては、循環論法ではないかと思わせるような局面が出てくるのはありえる話であろう。だが、それは、ナンセンスな批判されるべき論理学的な循環論法とは別のものなのだと思う。
千代島氏は、なんか、物理理論をあるいくつかの原理命題からの素朴な命題論理学の体系のように捉えてしまい、措定されているのは数理論理モデル全体なのだという認識が希薄なのではないだろうか。これは、千代島氏に限らず、安直にオルターナティブ物理理論を提起しては、混乱し、混乱させている諸氏にも、共通して言えるのではないかと私には思える。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・
「双子のパラドックス」のテーマとはずれるが、本章では、物理理論における論理モデルとは何かについての私なりの考察を以下、述べてみたいと思う。
私は、物理学(物理学に限らなくてもよいかもしれないが)が世の中に流布される論理形態は、次の四つの局面によって分類できるのでは、と思っている。
1.発見的推論モデル
物理学者が、未知の理論を模索している段階で展開される発展途上の論理。
2.体系的完全論理モデル
原理的な研究が一応完了し、原理から様々な具体的事例にまで、演繹的に展開できる論理装置の一連の体系を完成させた段階での論理モデル。
3.応用論理モデル
実用性という局面にスポットを当てて、原理的な最も抽象的レベルよりも、実際的によく使われる形態に特殊化し、そのレベルでの汎用性を残して、応用がしやすい形式にした論理モデル。
4.啓蒙的紹介論理モデル
物理学理論の啓蒙を目的に、単純で典型的な事例を選び出し、分かりやすく解説をするための論理モデル。
第一の「発見的推論モデル」というのは、例えば、前期量子論とかと呼ばれているボーアの原子構造モデルなどが挙げられるだろう。量子論の場合は、大勢の物理学者による長期にわたる発見的推論モデルの段階が続いた。しかし、場の量子論あたりで、相対性理論を加味した多次元のシュレーディンガー方程式が完成するあたりから、(存在論的な解釈をめぐる大問題が未だくすぶったままとは言え、)論理形式として一応の完成段階に到達した。つまり、安定した「体系的完全論理モデル」を獲得した。それは、工学的に有用な様々な「応用論理モデル」を基礎付けるものであり、「発見的推論モデル」に対しても、新たな視点からの再解釈ないし基礎付けがなされる。だが、これらの理論形式は、かなり専門的で、一般の人や初心者には馴染めないので、啓蒙を目的にした形で再構成された「啓蒙的紹介論理モデル」が提供される。これには、「発見的推論モデル」のいくつかが盛り込まれていたりすることもあるし、事例紹介という形で、代表的な「応用論理モデル」が取り上げられることもあるだろう。
もちろん、この分類は、ある時代断面に限って考えないといけない。「発見的推論モデル」には、当初から暫定的なものと自覚されて提起されるものもあるかもしてないが、物理学者は、常に「体系的完全論理モデル」の構築を目指して活動しているわけで、後にそれは「発見的推論モデル」にすぎなかったと評価されるというケースが多いだろう。また、ニュートン力学は、長い間、「体系的完全論理モデル」の地位にあったが、電磁気学や原子核物理学上の新発見等との矛盾を契機に相対論や量子論にその座を譲ることになった。そして、それは、大きな物理学史上の「発見的推論モデル」への位置付けがされると同時に、相対論や量子論のある条件下で成立する近似法則たる応用事例として、「応用論理モデル」への位置付けもされる形になる。また、物理学の入門者は、やはり、今でも、(多分これから暫くも、)ニュートン力学から始めるだろうという意味で、「啓蒙的紹介論理モデル」の一つとして位置付けられてもいると考えられる。だから、相対論や量子論が、将来、より広範囲に体系化され統一された完成度を増した理論に、「体系的完全論理モデル」の地位を明渡すことになることは充分ありうることだ。(すでにそうなっていると主張する人もいるかもしれない。)だが、現在、これだけ広範囲に検証され、応用されている理論なのだから、「応用論理モデル」として生き残らないということは非常に考え辛い。そして、以前のニュートン力学よりは広範囲な妥当性を持つという関係までが否定されることも考え辛い。
では、相対性理論に限定して、この4つの局面の論理モデルについて考えて見よう。
アインシュタインの特殊相対性理論が発表される前の、ローレンツやポアンカレらによる、エーテルをめぐっての諸学説、諸理論、これは、特殊相対性理論を「体系的完全論理モデル」とする視点からすれば、同時刻の相対性等の時間・空間に対するパラダイム変革をしない状態での数式モデルの提示で、「発見的推論モデル」であったと評価されるものである。そして、ここで提起されたローレンツ変換式は、特殊相対性理論の新たなパラダイムから、再導出される形で、吸収されることになる。ここでなされた論理モデルシフトは歴然としたものであり、光の媒体たるエーテルの存在という物理像は、完全に退くことになった。
だが、見落としてはならないのは、ここまで劇的ではないが、特殊相対性理論から、一般相対性理論に発展するところでも、明らかな論理モデルシフトが存在しているということである。そもそも、単なる相対性理論の前に「特殊」が付けられようになったのは、より大きな「一般」が出現したからに他ならない。この時点で、(特殊)相対性理論は「体系的完全論理モデル」から、「応用論理モデル」に移行しているのである。特殊相対性理論の枠組みから導かれたことは、一般相対性理論の見地から再解釈され再導出されているのである。
特殊相対性理論は、光速不変の原理と慣性系間の相対性原理という原理命題からの演繹体系として組み立てられた。ミンコフスキーは、これの幾何学的表現を与えたわけだが、この時点ではまだ、単なる数学的表現法の一つでしかなかった。しかし、一般相対性理論の見地からは、幾何学的表現は、むしろ本質的な位置付けになっており、(平坦ではない)四次元時空という概念抜きに考えることは、きわめて困難である。アインシュタインは、一般相対性理論を構築していく過程で、四次元時空概念を積極的に取り入れ、さらに非線形な幾何学にまで踏み込んでいったわけだが、ここで、物理的世界像のパラダイム変換がなされていったと考えるべきだと私は思う。つまり、ある単純原理からの運動学上の演繹体系という論理モデルは、時空幾何学モデルという形式に、「体系的完全論理モデル」の座を渡したのだ。
何故なら、一般相対性理論では、光速不変は局所慣性系に限定されたものに位置付けられ、ある原理命題からの演繹体系という様相ではなくなってきている。あえて言えば、幾何学上の公理命題の演繹体系等々と言えるのかもしれないが、結局のところ、運動学ないし力学は、幾何学に吸収された形になっている。そして、光速不変等の原理命題から演繹する論理モデルは、一般的には不完全なもの、ただ、歴史的には大いに評価されるべき「発見的推論モデル」だったと位置付けざるをえないだろう。
さて、ここから、「啓蒙的紹介論理モデル」について考えてみよう。まず、これは、厳密にどうあるべきかという制約が強くあるわけではなく、いかに語れば、物理学理論を分かりやすく解説、紹介できるかという視点で、解説者が工夫して築かれていくものであり、解説者の裁量に大きく依存する。そして、場合によっては、厳密性、正確性が犠牲にされることもある。
理学系の大学など、専門的な教育機関では、厳密な数式処理の鍛錬からやっていくだろうから、そういう教育を受けた人の場合は高度な数式から物理的意味を汲み取ることも可能だろう。一般相対性理論の「体系的完全論理モデル」から大上段に構えてやっていけばいい。しかし、そういう力量を身に付けた人はごく限られた人になるので、そのやり方では啓蒙には役立たない。それで、噛み砕いた単純化した事例や、イメージや、エピソードを織り交ぜて、色々わかりやすい解説が試みられる。しかし、「何をもって分かりやすさ」と判断するか、ということ自体、実は結構難しい問題だろう。いずれにせよ、どのような経緯で、その理論が発見され、構築されていったかを知ることは、その理論を納得していく上には欠かせないことだろうということから、多くの場合、「発見的推論モデル」が紹介される。初学者は、さしあたり、まず、この論理モデルの理解から入っていくことになるのだ。
さて、問題は、この段階で、すべてを理解しきってしまう人たちに生じる。そればかりか、そこから、推論し、矛盾を暴き出し、この物理理論は間違っているとまで、主張してしまう人もいるみたいだ。どこがどうおかしいのかは、もちろん、個別に具体的に指摘していくしかないのだが(でも、すでに行われていること)、とにかく、「発見的推論モデル」の部分的理解(誤解も混ぜた)で、一切を押し切ろうとする大胆さ(非謙虚さ)がその根底にあるのは、間違いない。
ただ、これも、一概に悪い現象ではないかもしれない。少なくとも、分からないのに分かったふりをしている人よりは、ずっと積極的に踏み込んだ熱意に満ちた人たちであること、少なくとも不誠実な人たちでないことは確かであろうと思う。
それにしても、不思議なのは、物理理論は、色々あるのに、「~は、間違っていた」式の批判を受けるのは、相対性理論が圧倒的に多いことだ。常識離れした展開という点では、量子論とかの方が、よっぽど、進んでいると思うが、相対性理論ほど、攻撃の対象にはならない。思うに、量子論の対象は、あまりに極微だから、常識離れした結論も容認できてしまうのかもしれない。(実際は、結構、マクロに現象することもあるし、生産現場や日常世界とも無縁でなくなってきているのだが。)しかし、相対論が扱うのは、日常生活の中でも、基底的とも言えるくらい重要な概念である時間と空間が対象になっている。確かに、光速という大変速い速度に近い速度での運動を扱うという意味で、日常生活のレベルから隔絶してはいるものの、惑星探査などが行われている今日において、そことの通信に何十分もかかってしまう光の速さは、それほど超絶たる速さだとは受け取れない。とにかく、時間と空間という日常的によくわかっているはずの概念についての了解が、覆されてしまっているということ、ここにこそ、相対論が攻撃の的になりやすい最大の理由があるのではないかと思う。
そういうことも、踏まえて、次章では、相対性理論が提起する物理的世界像である、四次元時空について、論じてみよう。
indexへ
8.ミンコフスキー時空図は発明か発見か
...
特殊相対性理論のローレンツ変換は、
ユークリッド幾何学の「四次元空間」における「座標の回転」
にほかならないことを発見した
...中略...
ただし、ミンコフスキーのこのようなとらえ方は、厳密に言えば「発見」ではなく「発明」であるということを見逃してはならない。これはある意味で非常に危険な発明なのである。なぜなら、ミンコフスキーは意図的に奇妙な「虚数の時間」というものを導入することによって、数学的な仕方で強引に時間を空間化し(時間を消してしまい)、四次元「時空」を四次元「空間」にしてしまったからである。
すなわち、
四次元「時空」(特殊相対性理論)
↓
数学的テクニックによって時間を消す
↓
四次元「空間」(ユークリッド幾何学)
というように、時間がミンコフスキーによって故意に(まさに単なる数学的テクニックによって)消されてしまうのである!
時間が強引に消されて空間になってしまったからこそ、四次元「空間」が可能になった。そして、四次元空間が可能になったからこそ、「ユークリッド幾何学の四次元空間における座標軸の回転」とローレンツ変換との関係が明らかになったのである。
また、その前に別の箇所(第3章 「特殊相対性理論における時間の本質」(p119))では、以下のように述べられている。
...
四次元時空という言葉を聞いただけで何か不思議なSFめいた現象を空想する人がいるが、これは単なる誤解であると言ってよい。四次元時空は文字通り「時間と空間の不可分性」を表現しただけのものであるから、それ自体が何か不思議な物理的現象をもたらすわけではないのである。
むしろ我々がここで注意しなければならないのは、四次元「時空」をいつのまにか四次元「空間」にしてしまう傾向があることであろう。時間が消えて空間だけの四次元になってしまうのである。
この傾向は、歴史的には数学者のH・ミンコフスキーに由来している。確かに、相対性理論における「時間」をある意味で「空間」として取り扱うことによって数学的な便利さが得られることは否定できない。しかしながら、単なる数学的テクニックによって時間そのものを消してしまうことは、時間の本質を完全にとらえそこなうだけでなく、我々人間にとって極めて危険な思想(たとえば、人間の自由を否定する硬直した決定論)をもたらすということを忘れてはならない。
なお、ここで、v が光速に比べて著しく小さければ、
本章では、千代島氏のこのミンコフスキー時空図についての見解を吟味することを通して四次元時空について考えてみようと思う。
千代島氏は、ローレンツ変換は否定していない。ローレンツ変換の幾何学的表現が、ミンコフスキー時空図になるわけだが、まず、ローレンツ変換について考えてみよう。
ローレンツ変換式は、ある座標系(S系)におけるある時空点(P)の座標(t,x,y,z)を、それに対して速度vで移動している別の座標系(S’)での座標(t',x',y',z')に変換する座標変換式である。ニュートン力学で、これに相当するのは、ガリレイ変換式で、x軸方向での運動に注目すると、
x' = x - v t
となる。これは、互いに移動している関係であれば、速度 X 時間の分だけ位置がずれるというごく初歩的な認識を数式表現したもので、常識的理解と何の矛盾もない。
ここで、時間座標(すなわち、時刻)については、特に何も言われない。どの座標系でも、時刻はすべて共通しているという前提が成り立っているわけで、あえて表現すれば、
t' = t
であるが、いちいちこんなことはニュートン力学では、明示することもなかった。これが常識の支えている了解である。
しかし、相対性理論では、この座標変換は、ローレンツ変換と呼ばれる以下の式になる。
t’ = γ (t - (v/c2)x)
x’ = γ (x - vt)
ただし、
cは、光速
γ = 1 / √(1-(v/c)2)
γ ≒ 1
v/c2 ≒ 0
となり、ガリレイ変換と同じになる。
ローレンツ変換では、時刻が、距離 × 速度/c2 だけずれるのである。そして、これこそが、相対性理論の革命的発見なのである。
ところで、cは定数である(光速不変の原理)。であれば、時間ないし距離の単位を、光速が1となるようなものを選べば、以下のようなよりシンプルな表現式にできる。
t’ = γ (t - β x)
x’ = γ (x - β t)
ただし、
β = v/c (光速を1として、その比の値で、速度を表現したもの)
γ = 1 / √(1-β2)
ここで、
t’ = γ (-βx + t)
x’ = γ ( x -βt)
と変形すると、以下のようなユークリッド空間の回転座標変換に大変よく似た形式になる。(ローレンツ変換を双曲線関数を使って表現すればさらによく似た形式になる。)
x’ = ( cosθx + sinθy)
y’ = (-sinθx + cosθy)
それで、ローレンツ変換が一種の回転のような一次変換として数学的に取り扱われるようにもなる。
また、時空間隔を計算する式
s2 = -t2 + x2 + y2 + z2
を見て、時間項だけにマイナスが付いているのが扱いにくいと思い、時間を虚数として定義してしまうと、上の式は、
s2 = t2 + x2 + y2 + z2
となって、これは、ユークリッド空間の三平方の定理に基づいた空間間隔を計算する式の単純な次元拡張とみなせるようになる。(ただし、これは、時間は実数、空間が虚数と定義しても目的は達成できる。だから、ここから、時間には虚数としての性質が本来的に備わっているかのような考え方を持つのはナンセンスである。こういう理解が結構流布しているみたいだから強調しておくが、ここに現れる虚数性は、時間と空間との間に横たわる関係属性の一表現形式であって、時間そのものの属性ではないことを理解すべきだ。時間自体はスカラー値で表現できるものであり、実数でも虚数でも連続数であれば、どちらでもいいのである。ただ、量子的「状態」の表現という局面になると、これは、複素数の範囲で考えなくてはならないから、虚数成分は、本質的に現れる。これは、ミンコフスキー時空の時間が虚数という議論とは全く問題の次元が異なる。)
このような経緯で、相対性理論は、四次元空間幾何学という形式で、表現され、計算処理されるようになったことは、千代島氏が指摘する通り、事実である。しかし、それでもって、時間を消してしまったとか、時間を空間と同じものにしてしまったと評価するのは、外観だけを見ての短絡的な発想である。
時間と空間は、相対性理論でも同じものではない。それは、数式の中にも表現されている。(時空間隔)2 は、(時間)2 と(空間)2 の和ではなく、差で表現せねばならないこと、もし和で表現したかったら、どちらかを虚数として定義しなくてはならないことも、その一つだ。
さらに、ローレンツ変換は回転座標変換に似た形式を持ちうることは確かだが、それは、一般的な意味での回転ではない。あえて言えば制限された回転である。回転を施せば、空間軸は別の空間軸に重ね合わせられる。しかし、ローレンツ変換では、空間軸を時間軸に、時間軸を空間軸に重ねることは出来ない。光速を超えられないという壁、幾何学的には、光円錐(超)面の壁がそれを阻止している。時間と空間が反転してしまうことは通常はありえない。(ブラックホールに突っ込むとか、途方もなく特異なことをしない限り。)この回転座標変換で空間軸が重ね合わせられるのは、空間軸のみであり、時間軸が重ね合わせられるのは、時間軸のみである。だから、空間はあくまでも空間であり、時間はあくまでも時間であり続ける。
それでも、千代島氏も認める、「時間と空間の不可分性」が、相対性理論によって発見されたことも事実である。ローレンツ変換では、時間と空間が加減算で結び付けられる。速度が掛けられているから直接的な加減算ではないかもしれないが、そもそも速度とは、光速に対する比の値として無次元の係数とみなせるものになっていることも加味すれば、かなり直接的に加減算で結合されていると見てよい。加減算で結び付けられるということは、両者はそれなりに同質のものであることを意味している。重さに温度を加えたり、身長から株価を引いたりする計算が全く無意味であるのは、全く異質な量どうしだからである。しかし、時間と空間とはそこまでも異質な量ではないということである。
確かに、ミンコフスキー時空図は、表現としては、視覚に訴えるために時間を空間化する形になっている。だが、空間を時間化する表現も、もしそれが可能であるならば、否定されるものではない。相対性理論は、時間と空間の量としての同質性の側面を明らかにしたのであって、一方的に時間を空間化したわけではない。
とにかく時空計量の一成分として位置づけられている以上、両者は、量としては同質のものとみなすのが、自然である。だが、一方で、我々の意識にとって、時間と空間がかなり異質なものとして現象することも、否定できない事実だ。私はこの異質性を否定するつもりはない。事実は事実として認めなくてはならない。
しかし、異質だから、異質なのだと言っていたのでは、かたや明らかにされてきた同質性との矛盾が解決されない。めざすべき方向は、何故、同質のものが、異質なものとして我々の意識に捉えられるようになるかを、客観的な時空構造等から具体的に解明していくことだと私は思っている。それに、この異質性にも様々な存在のレベルが対応しているだろうから、決して単なる物理学的側面等にのみ還元してもいけないだろう。だが意識への現象は、様々な存在のレベルが総体として渾然一体として現れるものであり、それを完全に概念的に再構成するには、自ずと限界もあって、直接的に把握された観念形態とのずれは避けられないだろうが、要はそういうアプローチの可能性を自覚しておくことが肝要なのだ。実際の日常生活において、直接的な観念形態で暮らすことをやめて、科学的概念の構成のみにもとづいて暮らしていくなんて、それは土台無理な話だ。
しかし、そういうアプローチを拒否し、ミンコフスキー時空という世界像は、時間・空間の異質性を忘れて、物理学者が、計算の便宜のために拵え上げた虚構物にすぎないと言い切ってしまう見方もあるだろう。たぶん、千代島氏は、こちらの見方を取るのだと思われる。だから、氏は、これは発見なのではなくて、発明品にすぎないと主張する。
私自身、相対性理論を最初に学び始めた当初は、そういう風に考えたりもしていた。しかし、同時刻の相対性についてじっくり考えていくうちに、過去から未来にいたるすべての時空点は、存在/未存在、決定/未決定等の属性で区別することは、(独我論のような立場を選択でもしない限り、)原理的に不可能だということに気が付いた。(それについては、拙稿「同時刻の相対性をめぐる諸問題」で展開した。)これを踏まえると、やはり、ミンコフスキー時空は発明ではなく、発見なのだと確信するようになった。つまり、存在しているのは、四次元時空であり、運動する三次元空間こそが、意識に現れる現象なのである。
科学は、一般に常識的な観念に対して、それが、よほど奇異な迷信などにもとづくものでない限り、単純否定する関係にはならない。むしろ、否定するのではなく、より根本的、普遍的立場からの基礎付けをするのであり、その観念の適用範囲を明確にするのである。時間・空間についての常識的観念は、ある意味で、日常生活の中で洗練された真実を担ってきているわけであり、単純に否定されるものではない。しかし、それは、日常生活範囲という限定された状況下でのことであることも受け入れなくてはならないわけで、適用限界を自覚することもまた豊かな認識へ向けての不可欠なステップなのだ。
・・・・・・・・・・・・・・
それほど昔のことではない。ほんの数百年前まで、我々にとって、大地が全体として球状をしていることは、仮説でしかなかった。ガガーリンが大気圏外から、自分の目で見て、地球のその丸さを実感してから、まだ半世紀も経っていない。もっとも、その時、彼は、地球の丸さではなく、青さに感動したようだ。この時点では、さすがに大地が丸いことは、人類の常識になっている。しかし、21世紀になった今日でも、自分の目で見て、地球の丸さを実感できた人はほんの一握りでしかない。それでも、「グローバル」化した現代、「丸い地球」という観念抜きでは、もはやまともな生活はできなくなっている。「丸い地球」は完全な日常生活意識の一部になっている。
地球の丸さを完全に実証したのは、世界一周航海を成し遂げたマゼラン一行だろうか。コロンブスの時代では、彼は、大地は平らだという通説と奮闘しなくてはならなかった。大地の丸さは、一般の常識ではなかった。
とは言え、大地が球状になっていることは、少なくとも、2千3百年以上も昔のアリストテレスの時代にはわかっていた。船の帆が上から見えてくることとか、月食は、地球の陰であってその形は丸いとか、根拠を挙げて証明されている。そんな昔から立てられていた仮説であるのに、世間一般の常識になるまでには、2千年以上もかかったのである。
それを思うと、「四次元時空」という観念は、それが生まれてまだ、百年足らずである。これが日常生活意識になるのは、おそらくかなり先のことではないかと思う。それこそ、今の我々が飛行機で外国旅行するように、恒星間旅行が出来るくらいの時代にならないと駄目かもしれない。そうなれば、「双子のパラドックス」のような現象は、当たり前のことで、日本が昼なのにブラジルが夜であることを何の疑問もなく受け入れられるごとく、受け入れられるようになっているかもしれない。
それまでは、四次元時空なんて信じられない、相対性理論は間違っている、等の風説が、コロンブスの時代でも、大地は平らで、まっすぐ行ったら地獄に落ちるという風説があったように、ありつづけることは、ある程度やむをえないことなのだろうか。
・・・・・・・・・・・・・・
最後に、四次元時空の考えが、「我々人間にとって極めて危険な思想(たとえば、人間の自由を否定する硬直した決定論)をもたらす」かどうかについて、簡単に触れておこう。というか、この問題は、そもそも簡単ではないし、本稿の主題とも大きくずれるから、ここで、この問題を論及するのは適当ではないと思っている。また、いずれ稿を改めて論じてみたい。だから、ここでは、本当に簡単にしか言わない。
私は、すでに拙稿「同時刻の相対性をめぐる諸問題」で、この問題に触れた。四次元時空の考えはある種の決定論ないし宿命論と呼べるものをもたらすと私は考えている。ただ、このレベルの議論で、人間の自由が否定されたり、肯定されたりするとは思っていない。もしそう捉えたら、それは、「人間の自由」に対して大変、浅薄で貧弱な思考しかしていないことだと思う。まず、自由とは何か、もっと踏み込んで根本的に考えてみることが必要だ。抽象的で無規定な自由意志とかを認めていさえすれば、自由を謳歌したことになると思っていたとしたら、それはナイーブすぎる。それと、思想の危険性とは何なのかということについても、よくよく熟考することもなく、安易に「危険な思想をもたらす」云々と判定してしまうことも、それこそよほど危険じゃないかと私には思えたりするのである。少なくとも、哲学的ではない。それでも、私は私なりに「危険性」ということを感じもし考えても来ていて、でも、その場合、取るべき道は単純な拒絶ではなく、より深い考察だと思っている。
indexへ
9.結び
やはり、こういう混乱を終結させるためには、「双子のパラドックス」の問題を、弟は地球、兄はロケットという前提をはずしての議論の形で展開してみるべきではないかと思うようになった。それで、本稿を起こすことにしたわけであるが、書物の批判というスタイルを取ったこともあり、関連していろいろ展開したくなったことも出てきたりして、当初予定していたよりも長めの論文になってしまった。
実を言えば、この本を買ったのは、かなり前で、その時は、論文まで書こうというほどの気は熟してなかった。最近、ウェブで、双子のパラドックス関連のサイトを検索しているうちに、やっぱり、双子のパラドックスって未だに混乱している、なんか論じなくては、という気持ちが高じてきて、それで、この本をひっぱり出してきた。その後、調べたら、この本は、出版社品切れになっていて、別の出版社で、「双子のパラドックスの論理」という題名でほぼ同じ内容で出版されていることに気づいた。各章の表題が若干変わっていたりするけれど、基本的に主張されている内容は同じだと思われる。以下にそちらの表題を掲げておく。
「双子のパラドックスの論理」
第1章 パラドックスの本質―何が問われているのか
第2章 ニュートンに立ち返って根源的に考え直す
第3章 特殊相対性理論と時間の問題
第4章 一般相対性理論と運動の問題
第5章 「矛盾」の論理的考察
第6章 なぜ従来の理論は失敗したのか
第7章 パラドックスを解決する手掛かり
第8章 パラドックスの最終的解決
新版は、「双子のパラドックスの最終的解決へと至る「論理」をいっそうわかりやすく鮮明にすることを目指して書き直した」そうである。ページ数は、313ページから201ページに減ってコンパクトになっている。(定価は高くなっているが。)しかし、冗長な表現やあまり重要でない弁舌部分が削られてまとめられているだけなので、本稿が取り上げた内容は基本的に継承されていると思われる。新版は、厳密な「論理的考察」をする力を鍛えるための教材として提供するという位置づけが濃いようである。
千代島氏の、物理学者の言っていることをただ鵜呑みにするのではなく、哲学的な視点で批判的に吟味していこうとする姿勢そのものは、私も大いに共感するところである。ただ、これでは、あまり厳密な「論理的考察」の手本にはなっていないのではないかと思われてならない。