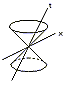
空間を3次元にした実際の4次元時空は、作図は我々には不可能で、数学的、形式的にしか扱えない。光円錐の「断面」の円(楕円)が、超立体の光円錐の球面(回転楕円体面)に相当しているような世界である。
しかし、ここで扱うのは、あくまでも、2次元の時空図である。
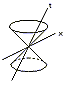 |
時空は、実際には4次元であるが、単純化のため、空間の次元は1次元にした。空間を2次元にした場合は、時空図は、光の世界線を垂直の軸を中心にして回転させたような立体面で、区切られた世界になる。この立体面は、2つ円錐形がの上下に向き合ったような形をしていて、光円錐と呼ばれる。 空間を3次元にした実際の4次元時空は、作図は我々には不可能で、数学的、形式的にしか扱えない。光円錐の「断面」の円(楕円)が、超立体の光円錐の球面(回転楕円体面)に相当しているような世界である。 しかし、ここで扱うのは、あくまでも、2次元の時空図である。 |