我々が、日々生活する中で、重力と無縁でいられることは、殆ど皆無である。現在、無重力状態を定常的に体験できるのは、スペースシャトルに乗る宇宙飛行士のようなごく限られた人しかいない。遊園地の絶叫マシンとか、バンジージャンプとか、いずれも、体験できる無重力状態は瞬間的なものだ。我々は、毎朝、目が覚めた時から、重力との格闘が始まる。陸上動物は、自らの体重に抗して、それを支え、移動させる力が生存のための基本条件である。海の中では、浮力が、空の上では揚力が、重力に対抗する筋力の助太刀をしてくれたりはするけれど、重力に抗することが、生存の基本であることに変わりはない。動物に限らず、植物も重力に抗して生きている。
　地上に生きるものにとって、かくも基底的な力である重力が何ものであるのかを理解することは、自らの存在の意味を知的に確認しようとするものにとっては、看過できない重要事ではないだろうか。しかし、そうは言っても、重力の何たるかを理解することは、今日、なんとも難しい状況にある。
　かつて、重力は、「何故」の対象にすらならない自明のものであった。物は、押しなべて、地面に向かおうとする目的を持っているものだ、重いものほど、強く（アリストテレスの自然学では速く）地面に向かおうとするものだと言い切っておしまいである。重力がそれ自体、解明されるべき対象になったのは、ガリレイやケプラーらの成果を集大成し、数学的な理論としてまとめあげたニュートンによる。およそ、物体間には、その質量に比例して、距離の二乗に反比例する万有引力なるものが働くという法則を打ち立て、重力は、力学が一般に扱う力の一種として位置付けられる。そして一般的な力学の法則、すなわち慣性の法則、力＝質量×加速度の法則、作用・反作用の法則に基づき、天体の運行からりんごの落下までをすべて統一的に説明することに成功したのである。
　この時に、地球と物とが引き合っているから重力という力が生ずるという重力観が確立された。これは、アインシュタインの一般相対性理論が登場するまで続く。ところが、一般相対性理論は、そんなに簡単に理解できないので、今日でも、大多数の人にとっては、重力は万有引力によって理解されているというのが実際のところではないだろうか。 　確かに相対性理論の一般向け解説書は数多く出され、ちょっと関心を持った人なら、「歪んだ時空が重力を生み出す」なんてフレーズを覚えていたりするのだろうけれど、なんで歪んだ時空が重力なんだ？（そもそも時空が歪むってなんなんだ？（というより時空ってなんなんだ？））という思いを引きずっている人が多いのではないだろうか。
　とはいえ、正攻法で、きっちりと数式を理解していくのも難儀である。アインシュタインの重力方程式は、最終的にまとめられた形はシンプルで美しいものであるが、そこに込められた意味内容にはとんでもなくややこしい関係が凝縮されている。あのテンソル方程式をもって重力というものを実感できる人は、かなり数学的・物理学的訓練を積んだ方であろうと推測する。私は、ギブアップ組の一人なので、この修行には耐えられない。
　しかしだ、先ほどにも述べたように、重力というのは、我々の生活の基底にあって常に格闘している相手であって、これが、なんだかよく分からないままでいるというのは、それはそれで、なんとも不甲斐ない。
　もっとも、物理学の最前線では、さらに進んで、ブラックホールや、宇宙誕生時のような超高密度の特異点の解明に向かっていて、そこでは一般相対性理論は無限大に発散するなどでお手上げ状態になってしまうらしく、４次元以外にさらにいくつもの次元を想定して理論を構築しているようだ。およそ、常識的観念は微塵もなく吹き飛んでしまっている世界である。そのような状況は、量子力学の世界で、すでにそうなっている。ただ、これらの場合は、対象そのものが、常識を超越した超極微、超高密度の非常識な世界なのだから、理論が常識的な観念と乖離して構築されたとしても、さしあたって、それほど違和感は感じなくてすむ（かのように思える）。
　しかし、相対性理論が扱う対象は、ごく日常的に接する、時間と空間と重力なのである。ニュートン力学が扱う時間・空間・重力と別種の時間・空間・重力が扱われるわけではない。確かに、非常識な値が顕著に算出されるのは、２１世紀初頭の人類の日常生活では、馴染みの少ない高速度や、強力な重力場であったりするわけだが、それは、単なる量的な違いであって、日常的なレベルと連続している。つまり、日常的なレベルでもこの世界像は適用されるし、されてしかるべきなのだ。
　私は、相対性理論を実感する、それは、４次元を実感することであり、そのための鍵になるのが、「同時刻の相対性」だという観点で、先の二論文を書いた。だが、記述内容は特殊相対性理論の基礎部分についてであり、一般相対性理論に及んでいない。そこを補う意味も込めて、なんとか、一般相対性理論をもっと実感的に把握できるように記述できないものだろうかとずっと考えてきた。

indexへ

　そこで、思いついたのが、真下に向かって「穴を掘る」ことである。穴を掘る。ひたすら掘る。掘って、掘って堀りまくる。どこまで掘るかといえば、地球の裏側に突き抜けるまで掘る。これである。
　青函トンネルの長さは５３．８５Ｋｍで、総工費約６９００億円（当時）、工期は２４年かかった。地球の直径は、約１万２千７百ｋｍだから、２３５倍の５６４０年くらい掛ければこの工事は完成するかといったら、そんな甘いものではあるまい。マントルや、核にかかる圧力に耐えられるような超強力な壁を作らなくてはならない。マリアナ海溝の水深１万１千ｍで、水圧は１１００気圧、この程度の圧力をなんとか克服できているにすぎない段階に人類はまだいるわけで、見通しはまったくもって暗い。恐らく、太陽系のあちこちに人類が基地を作るようになっても、この工事は企画すらされないであろう。
　だが、これは、あくまでも思考実験なのだから、技術的・経済的問題は一切無視して、遂行する。かくして、この想像を絶する困難を乗り越えて完成させたトンネルによって、何が実現できるかというと、地球上で考えられる限りの、究極の、自堕落な生活が実現できるのである。
　私は、重力を考えるのにアインシュタインが用いたエレベータによる思考実験が、どうも、生理的に好きになれない。何故かと言えば、綱の切れたエレベータに乗ったんでは、あれよという間に地面にぶつかって死んでしまうではないか。おちおち、重力のことなど考えていられるか？まだ、シュレーディンガーの考案した猫を閉じ込める箱の中に入った方がましというものだ。死と重ね合わせかもしれないが、観測されない限り半分は生きてられる。
　そこで考えたのが、エレベータを、先ほどの地球を貫通させた穴の上から落とすことである。（正確に鉛直方向に貫通していなくてはならない。）これなら、地面にぶつかる心配がない。地球の裏側に突き出たら、また戻ってくる。空気抵抗等の減速要因を除去すれば、半永久的に落ちつづけられる。これぞ、究極の自堕落生活である。
　ずっと、落ちつづけたいのなら、そんな大そうな穴を掘らずとも、スペースシャトルに乗って、地球を周回すればいいではないか、そちらのほうがお手ごろで格安であるとご指摘される方もおられることと思う。ごもっともなのだが、私がこだわりたいのは１次元の空間的動きなのである。周回したのでは、２次元の動きになってしまう。私は時空を考えたい。その最初のステップは、空間をまず、１次元で考え、そのレベルで明らかになることをはっきりさせた上で、空間次元数を上げていくという思考のステップを踏みたいのだ。従って、地球の自転の影響等も一切無視する。
　よく、一般相対性理論をイメージさせる図解として、薄いゴム膜を張って、そこに重い鉄球等を乗せて歪ませたような２次元面が示される。そこにパチンコ玉のようなものを転がして、中心の窪みに落ち込んでいくところを見せて、これが一般相対性理論の説く重力のイメージのように解説されたりすることがあるけれど、かえって分かりにくくさせているような気がする。あの図は、空間的な断面を表したもので、時空を表現してはいない。歪んだ空間のイメージとしてはいいかもしれないが、歪んだ時空のイメージには届かない。だが、一般相対性理論的に重力を考えるのに、一番重要で基本的なことは、空間の歪みではなく、時空の歪みなのである。

indexへ

　ところで、歪みというのは、歪んでないものがあって初めて語れるものである。歪んでない時空とは何か、それは特殊相対性理論で登場したミンコフスキー時空である。これは、本来、４次元なのだが、当面、１次元的な空間の動きのみに着目することにするので、２次元のシンプルなミンコフスキー時空図で考える。そして、さしあたっては、時空の歪みという発想は忘れることにしよう。
　ミンコフスキー時空では、物体（質点）は世界線と呼ばれる時間方向に伸びた線で表わされる。ある座標系で、その物体が動いているとすると、その世界線は、その座標系の時間軸に対して傾いている。物体が静止しているということは、世界線が、時間軸に平行になっているということである。加速（減速）運動していれば、その世界線は曲線になっている。
　それでは、地球を貫通した穴を落ちつづけるエレベータの世界線とは、どのようなものであろうか。それは、図に示すような、正弦曲線に似たようなものになるであろう。
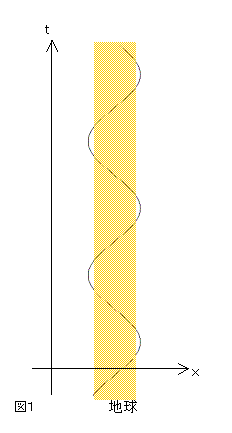　上空からエレベータを穴に向かって落下させる。どんどん加速されて穴に突っ込む。その後も速度は増して行き、地球の中心地点で、最高速度（秒速７．９ｋｍくらい）になる。だが、ここから減速が始まる。地球の裏側に突き抜けて所定の高さにまで達したら、方向を逆転してまた加速する。ここで加速度、すなわち速度の増し（減り）具合に着目すると、上空から、地表にいたるまでは、微妙に加速度は増していき、地中に入ったところから加速度は小さくなり始め、地球の中心点で、加速度は０になり、その後は逆向きの加速度が増加していく。そして、裏の地表を出ると加速度はやや減少し、ある最小値（その高さでの重力加速度）に達する。言葉で表現すれば、ざっとこんな運動をしつづけるわけで、世界線はくねくねと波模様を描いたような形になるはずだ。そして、この世界線上の観測者、すなわちエレベータに乗っているものは、ずっと無重力状態、宙に浮いた状態でい続ける。あたかも近くに何もない平坦な宇宙空間で慣性運動をしている系にいるかのような状態を体験する。
　一方で、近くに何もない平坦な宇宙空間で、この世界線とそっくりの動きを実現してみよう。それには、エレベータではなく、宇宙船に乗る必要がある。宇宙船はまず加速していき、徐々に加速具合を緩め、ある地点から逆噴射で、逆向きに加速していく、そしてまた逆に、というような往復運動を繰り返す。この運動は、形の上では、穴に落ちつづける世界線と同じ世界線を描く。だが、そこに乗る者は、加速とは反対の方向の後ろや前やに、引っ張られるような体験（慣性力の体験）をし続けることになるだろう。
　この動きをまず、ニュートン力学の世界観で考えてみよう。それに対して一般相対性理論はどのような世界観で、同じ現象を解釈するのかという筋立てで論じて行こう。ちなみに、この程度、すなわち地球の重力場程度のもとでは、ニュートン力学でも、一般相対性理論でも理論が返す数値には殆ど差が出てこない。比較するのは、あくまでもその考え方の違いについてである。

indexへ

　ニュートン力学で「落ちる」とは、引っ張られることである。物体間には、その質量（重力質量）に比例して、距離の二乗に反比例する引力が働く。この万有引力こそが重力の源である。では、例の穴に落ちる様をこの観点から具体的に考えてみよう。
　エレベータ（を構成する物質）は、地球を構成するすべての物体と万有引力で引き合う。その強さは、距離の二乗に反比例するわけだから、地球のすぐ近くの部分とは強く引き合い、遠く離れた部分とは弱い力で引き合う。エレベータを動かす力はそれら様々な部分との引力の合力である。この合力は、エレベータが地表の外側にある場合は、地球を構成する全ての物質がその重心（地球の中心と考えてよかろう）に凝縮したと仮定して、その質点との引力を逆二乗の法則で計算してやれば求められることが分かっている。ニュートンはライプニッツと並んで、微積分学の確立・発展に大きく貢献した人物だが、要は、例えばこのようなことを求めたいということがその動機であろう。引力は、距離が離れれば小さくなるわけで、地表すれすれの場所が最大の引力を及ぼす地点である。穴に突入してからはどうなるか？重心に近づくから引力は強くなるかというと、そうはならない。エレベータの位置より、上側の部分の物質は、地球の中心方向とは逆の方向に引っ張るわけだから、言わば、ブレーキの役割をし出す。合力の働き具合は、地表の外側とは趣が変わってくる。この場合、エレベータに働く引力の合力は、（地球の密度分布は球対称だとして）地球の中心からエレベータの位置までを半径とする球を構成する部分の物質が、中心に集まったと仮定して計算した引力の値に等しくなることが分かっている。従って、エレベータが地球の中心に来たときは、引力は０である。ここでは、すべての引力が均衡しあって差し引き０になるのだ。そして、中心を過ぎ去ると引力の合力は、逆向きになって次第に増加し、地表を突き出ると、距離要因だけになるので、引力は地表から離れるほど小さくなる。しかし０にはならないので、そのうち止まって、また地球の中心に向かって動き出すというわけである。
　次に、宇宙空間を宇宙船で往復運動する場合を考える。この場合、万有引力は関与しない。ここで働く力は、ロケット噴射による反発力である。（本質的には分子間に働く電磁気力に還元されうる力。）この力が宇宙船を動かす。しかし、物には慣性がある。つまり同じ速度の状態に留まろうとする性質がある。その大きさは質量（慣性質量）に比例する。力が働いて宇宙船が加速すると、その中の物体は、加速される方向と反対の方向に引っ張られるような見かけ上の力が働く。これを慣性力と言う。しかし、これは引力ではない。あくまでも見かけ上の力にすぎない、というのが、ニュートン力学での捉え方である。
　では、穴に落ちる場合は、この慣性力はどう現れるのだろうか。落ちる場合も万有引力という力で、エレベータが引っ張られるわけだから、そこに乗るものには同様に慣性力が働いてしかるべきだ。だが、事実は、慣性力は働かない。落ちる場合は、宙に浮いた状態になる。なぜか？宇宙船の場合は、力はまず船体に及び、船体の床なり壁なりが、そこに乗っているものに力を及ぼす。その反作用として、慣性力が現れるわけなのだが、落ちる場合は、そのエレベータの中のものすべてに直接、同等にその質量に比例した大きさで引力が働くのである。そして、どういうわけだか、万有引力の大きさを決める要因としての質量（重力質量）と、慣性力の原因たる、加速への抵抗を示す質量（慣性質量）とが、完全に比例しているのだ。これはエトヴィッシュによって高い精度で確認された。しかし、二つの量は、その定義上なんら脈絡がないわけで、どうして同じ扱いにできるものなのかは、ニュートン力学では、なぞであった。が、ともかくこういうわけで、落ちるエレベータに乗るものは、慣性力と引力が均衡して無重力の状態を体験し続けるのだと説明される。
　ところで、万有引力というのは、それ以外の一般の力と比べて異質な性格がある。それは、遠隔作用という点である。一般に力は、接触して伝わるもの、というのが、力学の基本前提である。その前提の上にニュートン力学は確乎たる体系を築き上げている。唯一の例外が万有引力なのだ。恐らく、ニュートン自身、気持ち悪かったのではなかろうか。しかし、そういう引力を想定して森羅万象が正確に説明でき、観測結果ともピタリと一致するという事実を前にして、疑う余地はなかったのだろう。
　ニュートン力学は、正確に事実を予測した。２１世紀の今日でも、その実用的価値は、殆どの場合、衰えていない。だが、その理論の世界観として、妙な気持ち悪さが残っていた。一般相対性理論は、観測事実がニュートン力学に矛盾したから生まれてきたものではない。その矛盾は、むしろ理論が完成されてから、（理論を裏付ける目的で）発見された。一般相対性理論は、観測事実によってではなく、旧来の理論の世界観的気持ち悪さにとことんこだわり抜いたが故に生まれたものなのである。

indexへ

　我々は、一般に、落ちることは、よくないこと、あってはならないこと、異常事態だという観念に基づいて生活している。落ちないように努力すること、それが日々の生活であり、生き残るための必須条件なのだ。
　だが、アインシュタインは、「落ち行くことこそ、自然なのじゃ」という地球人にはあるまじき、宇宙人的発想で開き直った。この開き直りが、一般相対性理論を実感するための第一歩である。
　「落ちてゆくのは、落ちてゆくべき力が働いている。」、「我々地上の物体は、地球の中心に向かって引っ張られている。そういう力が働いているから、落ちていく。」そのような考えを捨てるのである。そうではなくて、落ちていくのは、「何も力が働かないから落ちるのだ」と考える。先ほどから考えている、地球を貫通する穴に、落ち続ける姿こそ、（物理学的には）自然な姿なのだと。
　では、落ちないで、地表にへばり付いている我々は、不自然なのか、どう不自然なのか、ということになるが、それは、地表から上に向かって押されつづけているという意味で、常に、上空方向に加速され続けているという意味で不自然なのである。（なお、ここでは、「自然」「不自然」とは、慣性座標系にいる、いないという意味で捉えてほしい。）
　仕事を終えて、疲れた体でぐったりと横になったとき、目を瞑って、素直な気持ちで感じとってみよう。自分の体に加わる力は何かを。自分の体に触れているものは何だろうか、それは床だ。その床は、自分の体を地底の方向に引っ張っているだろうか。引っ張るために吸盤か何かで体を吸いつけているだろうか。そんなことはない。
　素直に感じ取れば、我々は上空に向かって押されつづけていることに気付くはずだ。これは、広大な宇宙空間で、加速しつづける宇宙船に乗っているときと同等の感覚である。単に感覚だけでなく、すべての物理現象は、地上に静止する系と、そこでの重力加速度相当の加速度で加速される宇宙船の系とでは全く同等に表れる。あるいは、宇宙空間で静止または等速度運動している系と、自然落下している系とは、物理法則は同等である、ということをアインシュタインは原理として打ち立てた。「等価原理」である。
　しかしだ、もし、地上にいる者は、加速的に押され続けているのだとすれば、地球は、加速的に膨張していないとおかしい。だが、地球のサイズは、不変である。インフレーション宇宙論は、聞いたことがあるけれど、インフレーション地球論なんてない。
　ここで、登場する概念、それが、「歪んだ時空」なのである。すなわち、地上のように、（地面の上と下とで）質量の分布状況が著しく不均一な場所では、時空は歪んでおり、その歪んだ時空に沿って「まっすぐな」世界線が、落ち行く世界線だと考える。（「まっすぐな」の正確な意味については後述する。）それに対して、地表にへばり付いている者は、歪んだ時空に対して無理して直進している世界線なのである。時空の形に素直に従わないで、そこから逸脱しようとし続ける。そのためには、力を加え続けなくてはならない。その力の源は何かといえば、それは、ぺしゃんこに潰れないように踏ん張っている、原子・分子間の電気的斥力に他ならない。日々、我々が体感する「重力」とは、実は「万有引力」なる引っ張る力なのではなく、原子・分子が踏ん張っている力なのだ。この力を我々は重力と呼んでいたのである。「引力」なんてものは実はどこにも存在していない、ニュートンのもたらした幻想だったのだ。現に何も引っ張っているものなどないではないか。やはり、離れた物質間で瞬時に働く遠隔作用というものを想定したのは間違いだったのだ。（ただし、それでもニュートンは偉いと思う。）

indexへ

　それでは、さっそく、この観点に基づいて、地球を貫いた例の穴に、落ちてみよう。
　まず、高い上空から、エレベータは、穴に向かって落ち始める。この時、加速されていくわけだが、厳密には加速の度合いは、上空ほど弱く、地上すれすれが最大になる。上空ほど、そのまわりの質量分布の不均一さがなだらかになっているからだ。ずっと上空、すなわち地球から遠く離れてしまったら、質量の分布状態は充分なだらかになって時空の歪みは殆どなくなる。重力場がないと考えられる地域、一般の平坦な宇宙空間である。
　一方、地球に近づけば近づくほど、そこを中心にして考えられる質量分布は、偏りが激しくなる。こういうところは、時空の歪みが激しくなっている。従って、加速的に落ちる度合い、すなわち、落ち行くものの世界線（＝時空の歪み具合に素直に沿った世界線）の曲がり具合が大きい。これが重力加速度の大きいことに対応している。地球の場合、地表面近辺が最大で、約９．８ｍ／sec²である。
　そして、穴の中に突入する。すると、この後、加速はされるのだが、その度合いが次第に小さくなっていく。これは、地球の中心に向かって地球の内部に潜り込めば潜り組むほど、その場所を中心とした質量分布の偏り具合が減るからだ。すなわち、時空の歪みがなだらかになり、落ち行くものの世界線の曲がり具合は小さくなる。そして、地球の中心地点では、完全に時空の歪みはなくなり、加速は０に、すなわち、等速度運動になる。（この時、速度は最大となる。）そして、こんどは、減速していくわけだが、これも、質量分布の偏りが逆方向に増し、時空の歪みが反対向きに増していくことに対応している。
　誤解のないように強調しておくが、存在する質量の量そのものが、重力場を出現させるわけではない。その場所を中心とした質量分布の偏り具合の大きさが、重力場を出現させるのである。地球の中心部は、高密度で、大量の質量に囲まれているのだが、重力場は０である。太陽の中心部だって０である。ここでは、質量分布は全ての方向について対称的となり、よって、ここの時空は歪んでいないのだ。
　もっとも、中心部の重力場が０であることは、ニュートン力学でも導かれる結論ではある。ただ、その思想的背景が違う。ニュートン力学の場合は、重力が均衡して相殺されているが故に無重力状態になっていると考える。一般相対性理論では、時空の歪みがなくなっているからだと考える。

（なお、ここで言う質量分布の「質量」とは、厳密には、４次元的な質量、４元運動量と呼ばれているもののことを指す。すなわち、エネルギーも質量の一種として、時空の歪みに関与する。これについては後述する。）

indexへ

　さて、これまでの話では、一般相対性理論特有の現象はででこなかった。考え方が違うだけで、ニュートン力学と結論は同じである。これでは、新しい理論を提起する価値があまりない。
　一般相対性理論特有の現象が顕著になるには、地球の重力場は、弱すぎるのである。つまり、時空の歪み具合が足りないのだ。これを強くするには、地球をぐっと圧縮する。思い切って、直径１センチ半くらいに圧縮する。この超超高密度な玉は、小粒ながら、目方は地球と同じだけあるわけで、そこから、地球の半径（約６４００ｋｍ）くらい離れた地点に対しても、今の地上で生じるのと同じ大きさの重力を及ぼす。言い換えれば、そこまで距離が隔たっても、時空を湾曲させる。従って、その距離から、この玉めがけて、物は落ちていく。
　それでは、落ちてみよう。そして、先ほどの地球に掘った穴に落ちていくときとの違いをみてみよう。
　穴に落ちていく場合は、加速される度合いが次第に小さくなっていった。だが、今度は落ちていくに従って、加速される度合いが、どんどん大きくなっていく。なんとなれば、質量の分布の偏り具合がさらに大きくなっていくからである。すると、速度は、はなはだしく増加していき、玉にぶつかる直前には、光速に近づいている。
　ここまでは、ニュートン力学でも同様の結論が出る。違いは、主として、時間に関して生じてくる。ニュートン力学では、時間は、座標系の速度とは無関係に、共通して一様に経過していくものである。すなわち、絶対時間の考え方を取る。しかし、特殊相対性理論で明らかになったことは、同時性や、時間の進み具合というものが、座標系に依存して変わる。光速に比較しうるくらい高速になると、それが顕著になる。この点の効果を考慮に入れなくてはならない。この玉に向かって落ちていくものは、上空で、落ちないで踏ん張っているものからすれば、光の速さに近づくにつれて、時間の進み具合が遅くなるように判断される。さらに、質量は増していく。そして、光の速さに達したところで、そこでの時間進行はストップしてしまい、質量は無限大になりもはや加速はされない。
　ただし、落ちていくものにとっては、こうはならない。上空で静止しているものからすれば、加速されていく系であっても、落ちていくものにとっては、その時点、その時点での固有時で考えるから、たんたんと時は流れて落ちてゆく。
　というより、落ち行くものこそ自然なのだ、という思想が、一般相対性理論なのだから、上空で、落ちないように静止している系の方こそ、加速度系というべきであろう。実際、落ちないように上空に静止していようとしたら、上空に向かって常に加速しつづけていなければならないのだ。（中心からの距離を一定に保ちたければ、周回軌道に乗れば、いいわけだけれど、あくまでも、ここでは、空間の移動は１次元に限定して考えてようとしているので、御了承願いたい。）落ちていくものにとっては、上空で踏ん張っているものは、どんどん加速的に離れていき、時間の進行がそのうちに止まってしまうように判断されるのである。
　このように、自由落下すると光速に至ってしまう半径をシュワルツシルツの半径と呼ぶ。これは、言い換えると、光速でないと脱出できないぎりぎりのラインでもある。この内側に入ってしまうともう光といえども出られない。さらに、この奥は時間と空間とが反転してしまうなど、奇妙なことだらけの世界である。言わずと知れたブラックホールだ。地球の場合は、この半径は７ミリくらいである。通常はこんな半径にいたるほど、物体を高密度に圧縮はできない。巨大な恒星が爆縮した時とか、宇宙創生の時とかに出来るらしい。一般相対性理論の重力方程式（偏微分方程式）の一般解（原始関数）が始めてもとめられたときに分かったもので、シュワルツシルツは、第一次世界大戦の戦火の中で計算していたというから、すごい頭の持ち主がいるものである。

indexへ

　ところで、これまで、時空の歪みについての話はしたが、空間を１次元に限定して考えていたので、空間としての歪みについては何も語らなかった。だが、地球が、ここまで小さなサイズに圧縮されたとなると、この問題も見過ごすわけにはいかない。
　地球は落ちていくエレベータよりもずっと小さいのである。この球体に近づけば、落ちていく方向が、エレベータの右と左とでは違ってしまう。つまり、エレベータは、横方向に圧縮される。さらに、エレベータの下と上では、重力場の大きさが異なり、下の部分の方ほど速く落ちようとする。つまり、エレベータは縦方向に引きちぎられてしまう。もちろんそこに乗っているものも同じ運命であり、およそ落ちていく物体は、ばらばらになってしまう。（これを潮汐作用という）
　これが、極度に歪んだ空間の事例である。では、本来の地球においてはどうかといえば、地球サイズのゆるやかさで、空間は歪んでいるのだ。一般相対性理論では、落ちていくものが、その時空の曲がり具合に沿った世界線をなす。今までは、重心に向かって、まっしぐらに落ちていく姿ばかりを扱って来たが、弧を描いて落ちることも、地球を周回することも、落ちる姿のひとつである。地上から真横に、第一宇宙速度（７．９ｋｍ／sec）で、飛んでゆけば、地面にぶつかることなく落ちつづけられる。この世界線は、螺旋状の形をしているばずである。（２次元の空間と１次元の時間の時空において。）このように、重力のあるところでは、慣性系が曲がった世界線の形をなす。重力場のない平坦な時空であれば、直線的な世界線が慣性系である。このように、落ち行くものの世界線を思い描くことによって、大雑把なりに、時空の歪み具合というものをイメージできるのではないかと思う。
　地球の重力場では、空間の歪み具合は、地球のサイズでないとわからない。要は地球の丸さが感じ取れるかということなのである。どこまでもほぼ平面的な大地が延々と続いているようにしか感覚できないはずだ。人間が身体で行動できる範囲のサイズでは、重力場は大きさも方向も一定に思えてしまう。それが場所や高さで異なることを自覚するには、人間の身体は小さすぎるのである。
　それに対して、時空の時間的歪み具合は、やけに体感しやすい。地上において、一秒の間に、落ちる速度は、９．８ｍ／sec増加する。地球を貫通させた穴に落ちていくのに、大して時間はかからない。４２分くらいで地球の裏側に達する。その間に重力加速度の大きさと方向は劇的に変化する。
　なぜ、空間的な歪みはなだらかなのに、時間的な歪みは激しいのだろうと思ってしまう。だが、これは、単位系の問題なのだ。我々は、例えば、長さをメートル、時間を秒という単位で測る。そして、秒とは瞬時の時間間隔だという感覚で生きている。しかし、相対性理論の世界では、光の速さが１となるような単位系が、理にかなった単位系である。こうすると空間的なものと時間的なものとが対称的に表現でき、シンプルな数式でまとめられる。例えば、長さの単位をメートルとすれば、時間は３億分の１秒（約３ナノ秒）が１単位の時間だ。１メートルの時間と言ってもいいかもしれない。(※)
　この単位系で考えると、１秒の長さは、光が約３億メートルも進むという、大変長い時間である。そんな長い時間を一瞬の時間としてしか感じ取れないくらい、人間の時間感覚は鈍いのだ。（他の地球上の動物も恐らく似たり寄ったりだろう。）だから、同時刻の相対性は感じ取ることはできず、相対論的効果は、日常生活の感覚とは縁遠いものになってしまう。
　ところが、この鈍感さが、時間方向での時空の歪みに対する敏感さを提供するのである。１Ｇの重力加速度とは、９．８ｍ進むのに１秒（３億ｍ）もかかる速度を達成するのに１秒（３億ｍ）もかかるという加速度である。光速＝１の単位系で考えると、９．８ｍ／sec²は、１．０９×１０^-16という値である。３億分の１秒の時間を基準で考えたら、地上で、物が落ちる速さは極めて遅い。落ち行くものの世界線（光速＝１のミンコフスキー時空でのそれ）は、殆どまっすぐであり、時空の歪みを感知するのは困難である。
　だが、我々は、１秒を一瞬の時間としてしか感じ取らない。だから、重力を感じ取ることが出来るのである。そして、一般相対性理論的に言うと、重力を感じ取れるということは時空の時間方向の歪みを感じ取れるということを意味するのである。

(※)
　３ナノ秒は人間の心にとっては大変短い時間だが、１秒間に何百万もの命令をこなせるコンピュータにとっては、そんなに短い時間ではない。人類の技術は、今やフェムト秒（千兆分の一秒）を相手にしている。光が０．３ミクロンしか進まない時間である。現代の人間の労働力にとって、３ナノ秒なんてちっとも短い時間ではない。（なお、もし、時間の単位を秒にしたければ、長さの単位を１光秒＝３０万ｋｍにしても光速＝１の単位系になる。時間の単位を年、長さの単位を光年にした単位系は、天文学でよく使われる、光速＝１の単位系の代表例である。）
indexへ

　これまでのところ、「時空の歪み」というのを単に言葉でしか表現してこなかったので、その意味はとても曖昧だったと思う。厳密には数式で表現すべきものなのだろうが、数学の訓練を積んでいない我々には、大変苦しい道である。やはり、なんらかのビジュアルなイメージが媒介されないと辛い。
　しかし、歪んだ３次元、４次元の空間（時空）をイメージすることは、原理的に不可能だ。われわれのイメージ可能な空間の歪みは、せいぜい２次元の面の歪みまでである。歪みというものを鳥瞰するには、１つ高い次元に立っておく必要があるからだ。（ただし、歪みの数学的表現方法は次元の高みを必要としない方法でなされる。２次元曲面の歪みは２次元の中で定義される。）我々は、２次元の歪みのイメージを手がかりにして、それを超える次元については数学的な形式を頼りに探るしかない。
　我々が、通常イメージできる歪んだ２次元空間は、球面のようなものである。あるいは馬の鞍のような形をしたものもある。ただ、筒状の形、紙や鉄板を単純に丸めたり曲げたりしただけのような形は、曲がったものかも知れないが、歪んだ２次元空間の部類には含まれない。伸ばせば平面になるものは、歪んだものとは扱わないのである。しかし、紙にお茶かなんかをこぼしてでこぼこになったものとか、鉄板をハンマー等で叩いて、窪ませたりしたら、それは、歪んだ２次元空間に仲間入りする。まあ、こんな感じで、空間的な面の歪みはイメージしやすい。
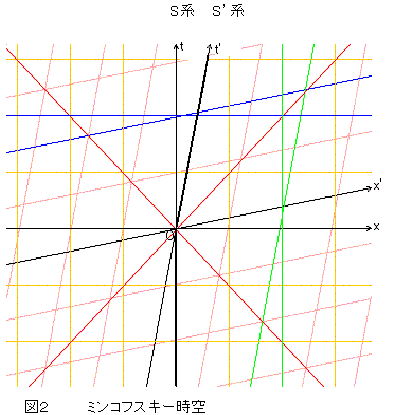　問題は「時空」だ。そもそも歪んでいようがいまいが、「時空は」見えない。それを敢えて見える形にしたのが、ミンコフスキー時空図である。これが歪むのである。では、どう歪むのか？そして、重力場とその歪みはどう関連しているのだろうか。
　図２では、２つの座標系が示されている。点Ｏで、Ｓ系（図では直交系）から、Ｓ’系（図では斜交系）に移るような世界線があるとしよう。これは、時空点Ｏで、瞬時に速度を変えた加速度系である。（現実には滑らかに速度は変化してしていくだろうが、ここでは単純化のためこうする。）時空点Ｏで、強い力が加わり、世界線は折れ曲がった。この世界線に乗るものは、このとき強い慣性力を体験したであろう。また、同時刻のラインがｘ軸からｘ’軸に変わってしまい、右側遠方にいる者の年月が一気に経過してしまった状態になるだろう。(いわゆる、双子のパラドックス効果。)加速度系は、このような平坦なミンコフスキー時空内で曲がった世界線に乗った系のことである。
　次に、この図（次の図３）を紙に印刷するなどして、はさみとのりを用意してもらいたい。そして、点Ｏから右上の部分のｔ軸とｘ軸に切り込みを入れて、色のついた部分をのりしろにして、ｔ軸とｔ’軸、並びに、ｘ軸とｘ’軸がぴったり一つの線に重なるように貼ってもらいたい。それがすんだら、点Ｏから左下の部分のｔ軸とｘ軸に切り込みを入れて、色のついた部分をのりしろにして、ｔ軸とｔ’軸、並びに、ｘ軸とｘ’軸がぴったり一つの線に重なるように貼ってもらいたい。
　でこっと歪んだ面が出来たと思う。手前に突起させるか、向こう側に窪ませるかは、どちらでも構わない。歪んだ２次元面としては、同等の扱いである。これが歪んだ時空図の最も単純な基本形である。この図の右上、左下部分は、斜交系、左上、右下部分は直交系である。ここで、二本の時間軸、空間軸は一本になった。この時間軸・空間軸に基づいた座標系は、直交系でもあり斜交系でもあることになる。もし、右上、左下部分を直交系で表現したら、左上、右下部分は斜交系にならざるをえない。歪んでないミンコフスキー時空の座標系では、任意の斜交系は直交系に直して考えることが可能であった。しかし、この歪んだ時空面は、全ての部分にわたって直交系に変換することは不可能なのである。
　なお、この歪みによって、（３次元に住む我々には）ｘ軸に垂直な方向に時空は突き出るもしくはへこむように見えるけれども、表現されているのは、あくまでも、ｔ軸とｘ軸による２次元時空であって、ｙ軸、ｚ軸方向とは何の関係もないということは、理解しておくべきである。
　さて、ここで作った、歪んだ面に対して、定規を当てて、直線を引いてみる。最初、下側の時間軸に平行になるような線を引き、それをそのまま、まっすぐに上へ引き伸ばしてみよう。するとどうなるか、上側にいくと、時間軸と平行ではない線を引くことになるはずだ。このまっすぐな線こそは、重力場で落ちないように踏ん張るものの世界線にほかならない。これは、歪んでない時空の時間軸に平行な世界線を意味する。
　時間軸に沿って（もしくは時間軸に対する傾き（＝速度）を一定に保って）進む世界線こそが、歪んだ時空に素直な世界線、すなわち、落ち行くものの世界線なのである。それに対して、落ちまいと抵抗するには、力を加えて、時間軸に対する傾きを変えてやらなくてはならない。こうしてはじめて歪んでない時空の時間軸と平行を保つことができるのだ。だが、それには力を加えて加速しなくてはならない。つまり、歪んだ時空においては、落ちないでいる系は、加速系なのである。
　ここで、提示した時空図は、一点Ｏで、瞬時に折れ曲がるという単純形であるが、現実の自然界にこんなカタストロフィー的時空は存在しないだろう。実際は徐々に、滑らかに曲がっていく。そこのところは、微分学の活躍する場面である。しかし、ややこしい数学は、良書にお任せして次に進もう。

indexへ

　さて、時空内を自然落下する世界線とはどんな線なのかをもう少し正確に言うと、ある点からある時空的方角（速度）が与えられた場合、その時空の測地線を表すと言われる。この測地線は、歪んでいない時空では、直線である。時空が歪んでいると、ある特定の曲線になる。どんな曲線になるか。
　測地線の身近な例は、地球儀の大円コースである。このコースは、２点間の最短距離を表す。もっと複雑な形状の曲面の場合、必ずしも、測地線は２点間の最短コースではなかったりするのだけれど、まあ、シンプルな曲面では、最短コースが測地線と考えてもよかろう。これと同じ考えで、歪んだ時空では、最短時間のコースがその時空の測地線と考えてよいかというと、そうではない。逆で、最長時間のコースが測地線を表す。この点は、結構、誤解されがちのような気がするので、説明しておくべきだろう。
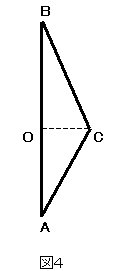　 誤解されやすいのは、図でみると、一見最短時間コースのように思えてしまうからだろう。まず、歪んでない時空の場合で考える。図４で、ＡＯＢというコースと、ＡＣＢというコースのどちらが短い時間か？答えはＡＣＢの方が短い時間を表している。
　「なんで？」と思った人は、ユークリッド空間の計量構造に囚われた正常な常識人である。しかし、ここは、たとえ歪んでいなくとも、ユークリッド空間とは、ちょっと趣の違うミンコフスキー時空である。
　ユークリッド空間の世界では、ＡＯと同距離、ＢＯと同距離の軌跡を描けば、図５のように円弧になるわけで、ＡＣ＞ＡＯ、ＢＣ＞ＢＯの関係が成り立つから、ＡＣＢ＞ＡＯＢである。

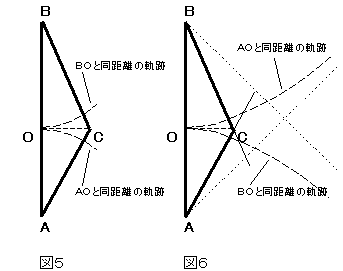　しかし、ミンコフスキー時空では、ＡＯと同距離、ＢＯと同距離の軌跡を描くと、図６のような、（光の世界線を漸近線とする）双曲線を表す。すると、ＡＣ＜ＡＯ、ＢＣ＜ＢＯの関係になって、ＡＣＢ＜ＡＯＢとなる。
　ＡＣＢのコースの世界線は、加速度系である。双子のパラドックスでは、宇宙旅行をして戻って来る側である。ＡＯＢは、動かないでじっと帰りを待っていた側である。宇宙旅行（加速度運動）をした方が、経過時間は短い、つまり年の取り方が遅いということになる。一般に、加速度系は、慣性系より固有時間が短い。慣性系は最長時間（時の刻みのテンポが最速）のコースなのである。だから、時空内の測地線とは、（この場合、）空間的には最短、時間的には最長のコースとなる世界線のことである。
　では、歪んだ時空の場合はどうか、というと、やはりその時空で、空間的には最短、時間的には最長のコースとなる世界線が測地線である。（ただし、時空の歪み具合が充分にシンプルに考えられる範囲内で。）落ち行くものの世界線は、これに該当し、地表にへばりつくものの世界線は、加速度系のように経過時間が短くなる。もし、人より長生きしたいのなら、過激な宇宙旅行をしなくても、強力な重力場の地表で暮らす方法でもよいわけだ。

　ここで、２点間の隔たりということについて、もう少し詳しく述べよう。
　空間内のある点からある点までの距離、それは、どんな座標系を選ぼうと一定不変である。ユークリッド空間では、ｘ、ｙ、ｚ軸をどう選ぼうとも、（三平方の定理により、）各空間成分の２乗の和が、２点間の距離の２乗に等しいという関係として表現される。
　これは、ある原点から一定の距離にある点の軌跡は、円（球面、超球面）で表されるとも言い換えられる。
（方程式にすると、(ｒ)²＝(ｘ)²＋(ｙ)²、あるいは、ｘ＝r cosθ，ｙ＝r sinθ　（ｒは距離、θは方角を表すパラメータ））
　これに対して、ミンコフスキー時空は、（歪んでないという意味でユークリッド空間と同類ではあるが、）２点間の距離の定義が少し異なっている。それは、時間成分の２乗と空間成分の２乗との和ではなく、差が、２点間の隔たりの２乗を表すという構造になっている。
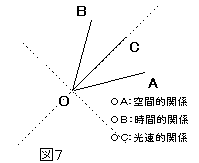　 時間成分の方が大ならば、２つの時空点間は時間的関係にあり、差の平方根は、２点間が同地点とみなせる座標系での時間を意味する。一方、空間成分の方が大ならば、２つの時空点間は空間的関係にあり、差の平方根は２点間が同時刻とみなせる座標系での距離を表す。差がゼロの場合、即ち、空間成分と時間成分とが等しい場合２点間は、光速で移動しなくてはならない位置関係にあり、時間的にも空間的にも隔たりは零である。すなわちこの２つの時空点は、同時刻かつ同地点の関係にあり、およそ、時間の経過とか、空間的隔たりとかの概念が適用できない位置関係にあると言わなくてはならない。
　これは、ある原点から一定の隔たりにある点の軌跡は、光の世界線を漸近線とする双曲線で表されるとも言い換えられる。
（方程式にすると、(ｓ)²＝(ｘ)²－(ｔ)²、あるいは、ｘ＝r coshφ，ｔ＝r sinhφ；　または、(τ)²＝(ｔ)²－(ｘ)²、あるいは、ｔ＝r coshφ，ｘ＝r sinhφ　（ｓは距離、τは時間、cosh、sinhは双曲線関数で、coshφ＝(ｅ^φ＋ｅ^-φ)／２、sinhφ＝(ｅ^φ－ｅ^-φ)／２、φは時空的方角である速度に対応付けできるパラメータ（tanhφ＝sinhφ／coshφ＝ｖ）））
　このような、計量構造は、同時刻が座標系によって、異なるというミンコフスキー時空の特性から来るものである。ちなみに、ニュートン力学での絶対時間の考え方に従えば、時空計量は、加速度系も慣性系も不変である。先の図では、ＡＣＢ＝ＡＯＢである。ある原点から一定の隔たりにある点の軌跡は、ｘ軸に平行な直線（方程式は、τ＝定数）で表せる。

　（ちょっと、分かりづらい話になってしまった。原点から等距離を表す点の軌跡が、光の世界線を漸近線とする双曲線になることは、当サイトの「Minkowski時空座標系の動き 」の座標軸の傾きを変えてみて、同時刻（地点）ラインと座標軸との交点の軌跡を考えてみてもらえばイメージできると思う。）
indexへ

　相対性理論で、一番有名な公式はといえば、やはり、Ｅ＝ｍｃ²であろう。こういう題名の山口百恵の歌もあるくらいだ。（そんなのも知っているなんて、ひょっとして、結構オタクではないかって？そんなことはどうでもよろしい。）
　しかし、なんで、質量に光の速度を２回掛けるとエネルギーになってしまうんだ？と不思議に思っていないだろうか。式は知っていても、その意味までわかっているわけではない人は結構多いと思う。
　この節では、そこのところを解明しておこう。ただし、この節のテーマは、運動する質点の幾何学についてである。さしあたり、特殊相対性理論の枠組み内で成立する内容のことになる。従って、歪んだ時空のことは、ひとまず忘れてもらってもかまわない。
　これまで、世界線についてあれこれ述べてきた。世界線とは、運動する質点の４次元的表現である。（私は、こちらの方が運動する物体という表象のより客観的表現だと思っている。）質点という概念は、物体の位置、時刻、速度の他に、「質量」という属性を持った抽象概念である。従って、世界線についても、「質量」属性を付けて考えねばなるまい。
　この質量とは、さしあたり、時空を歪ませる質量（重力質量）ではなく、世界線を曲がりにくくさせる質量（慣性質量）である。世界線が曲がるということは、力が加えられて質点を加速運動させられることを意味する。重い（質量の大きい）世界線というのは、容易な力では曲がらない世界線のことだ。世界線の質量の大小は、太い剛直な針金か、細いしなやかな針金かでイメージするとわかりやすいかもしれない。
　この世界線を幾何学的に分析する。世界線の接線ベクトルを考える。その長さを１としよう。単位は、例によって、光速が１となる単位系で考える。この単位系では、速さは光速に対する比率で表現される。
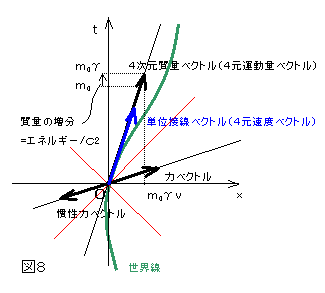　 　さて、この接線ベクトルの長さが１ということは、時間軸がその接線に平行な座標系、すなわち質点の速度が零となる座標系で、測って１ということである。だから、その接線に平行でない座標系（相対速度がｖの座標系）では、時間成分がγ、空間成分が、γｖで表される。（ここで、γ＝１／√（１－ｖ²）　従って、γは１以上の値）これは、特殊相対性理論の基本的な帰結で、走るものの時間単位は間延びする（時計の進行が遅くなる）ということからくる。
　つまり、世界線の単位接線ベクトルは、それが速さｖとなる座標系では、（ｔ，ｘ）＝（γ，γｖ）である。これに世界線の質量を掛ける。この質量とは、世界線が静止した状態に見える座標系で、測った、加速のしにくさであり、静止質量という。なぜ、こんなややこしい言い方をするかと言えば、運動している物体は光速に近づくほど加速しづらくなる性質があるからだ。静止質量は、世界線をどの座標系でみるかによって変化することのない、世界線固有の属性である。この静止質量ｍ₀の長さをもつ世界線の接線ベクトル、
　Ｍ　＝　（ｍ_t ，ｍ_x）＝　（ｍ₀γ ，ｍ₀γｖ）
を考える。これは、４元運動量と呼ばれたりしている。だが、単位は、質量の次元なので、４元質量ベクトルとでも言ったほうがいいかなと思うこともある。
　これは、世界線のある点における勢いのようなものを表現している。というのは、この時間成分は、エネルギー、空間成分は運動量を表しているからだ。
　なんとなれば、γ＝１／√（１－ｖ²）をテーラー展開すると、（ｖ≪１で、）γ≒１＋(1/2)ｖ²だから、ｖが光速（＝１）よりずっと小さな速度であれば、
　　ｍ₀γ　≒　ｍ₀　＋　(1/2)ｍ₀ｖ²
　　ｍ₀γｖ　≒　ｍ₀ｖ　　　　　（ｖ³は０とみなせるくらい小さいので無視する）
となる。上の式の第２項は、ニュートン力学で定義された運動エネルギーであり、下の式は、ニュートン力学で定義された運動量である。
　４次元的な質量ベクトルの時間成分の増分は、運動エネルギーだった。運動エネルギーに対応した質量が、静止質量に追加されたのである。だから、この時間成分を一般に「質量」として定義すれば、速度とともに、「質量」は増すということになる。
　ここで、運動エネルギーは、質量の次元をもって表れるが、それは単位系のとり方を光速が１となる単位系にしたからである。単位系をｍ・ｋｇ・秒のＭＫＳ系にするならば、上記のｖは、ｖ／ｃ（ｃは光速）に置き換えればよい。すると、
　　ｍ_t　≒　ｍ₀　＋　(1/2)ｍ₀ｖ² ／ｃ²
　　ｍ_x　≒　ｍ₀ｖ／ｃ　　
　これを変形すれば、
　Ｅ　＝　(1/2)ｍ₀ｖ² 　≒　（ｍ_t　－　ｍ₀）ｃ²
　Ｐ　＝　ｍ₀ｖ　≒　ｍ_x　ｃ
となる。ここで、（ｍ_t　－　ｍ₀）は、質量の増分で、それを、ｍとおけば、あの有名な公式
　Ｅ＝ｍｃ²
が、導き出せる。光速を２回掛けることになったのは、γ のテーラー展開の第２項が用いられ、そこで速度が２乗されていることと、単位系をＭＫＳ系にしていることとに基づいて生じたことである。本質的な理解としては、そもそも、エネルギーというものは、質量の増分のことだ、ということである。ひるがえって、増加する前の静止質量 ｍ₀も、エネルギーを足しこめるものなのだから、エネルギーと同等の性質のものではないかとも言えるわけで、相対性理論は、質量とエネルギーは本質的に同じものであり、４次元質量ベクトル（４元運動量ベクトル）の時間成分のことなのだということを解明したわけなのである。
　Ｅ＝ｍｃ²という式が有名であることは、核反応時の質量欠損が、反応時のエネルギーに対応していて、原子爆弾の基礎付けをされたかのように言われていることが、大きな理由の一つだろう。もっとも、相対性理論から、原子核反応の仕組みは導き出せない。相対性理論は、原子核反応に限らず、普通の化学反応でも、エネルギーの出入りが質量の増減になっていることを一般的に解き明かしたにすぎない。例えば、熱エネルギーは、構成分子の運動エネルギーであり、従って４次元質量ベクトルの時間成分の増分なのだ。しかし、通常の化学反応で得られるエネルギーに対応した質量の変化は、あまりにも小さすぎて、認識できない。光速に比較できるような大きな速度を伴う運動でないと、質量の変化は捉えられない。ニュートン力学では、エネルギーや運動量といった、別系統の概念で、この質量の微小変化に対応した現象をクローズアップさせてきていたのだとも言えるかもしれない。あるいは、こうも言えるかもしれない。このような微小な質量変化を、エネルギーのような概念を対応させて扱わなくてはならないほど、我々は時間経過に対する感受性が鈍感なのだと。一秒というのが一瞬であるが故に、我々にはエネルギーが大そうなものとして迫り来るのである。（あるいは、１光秒（３０万ｋｍ）の空間単位に比べて我々の身体は、非常に小さいが故に、わずかな質量変化でも感じ取れてしまうからだ、という言い方もできるかもしれない。）
　かくして、速度は、世界線の傾き、加速度は世界線の傾きの変化率、エネルギー・運動量は、静止質量分の長さの世界線接線ベクトルの時間・空間成分、と言う具合に、おしなべて、運動する質点の力学は、世界線の幾何学に置き換えて考えられる。相対性理論は、力学を幾何学にした理論なのだ。特殊相対性理論において、すでにそうなのである。
　では、「力」はどうなるのか、それを最後に説明して、この節を終わろう。
　力は、４次元質量ベクトル（４元運動量ベクトル）を微分（全微分）したベクトルで表される。ベクトル解析学によれば、接線ベクトルを微分すると、法線ベクトルになる。法線とは、接線に直交する線である。ただし、ここは、ミンコフスキー時空なので、「直交」の意味に注意しなくてはならない。ユークリッド幾何学での直角方向で理解してはならない。ここで、「直交」する方向とは、もとの線が時間軸と捉えられるなら、そのような座標系の空間軸方向のことを意味する。逆に、もとの線が空間軸と捉えられるなら、そのような座標系の時間軸方向のことを意味する。従って、世界線の接線ベクトルは時間方向だから、その方向を時間軸とする座標系の空間軸方向に伸びたベクトルが力ベクトルである。
　（直交の意味が再定義されているわけだから、ベクトルの内積の意味とかも再定義される。この辺の詳述は省略する。）
　世界線が、ずっと真直ぐに伸びていたら、その微分、つまり力ベクトルは零である。世界線が曲がっていたら、曲がっている方角の空間軸に沿って、力ベクトルは表れる。正反対の方向に同じ大きさを持つベクトルは、その加速度系にかかる慣性力を表す。
　ちなみに、単位接線ベクトル（４元速度ベクトルとも言う）を微分したベクトルは、加速度ベクトルである。力ベクトルは、このベクトルと方向が同じで、静止質量倍の大きさである。ニュートン力学の、力＝質量×加速度　の法則の４次元版である。

　ここで、ちょっと、哲学的な問題。世界線が曲がるのは、力がそこに働くから曲がるということなのだろうか？それとも、曲がった世界線がそこに存在しているから、そこに力というものが認識されるということなのだろうか？
　この問題、また後で考えることにして、とりあえず、次に進もう。

indexへ

　質量の軽いしなやかな世界線は曲がりやすく、質量の重い剛直な世界線は曲がりにくい。だが、その剛直さは、単に自らの曲がりにくさを主張するに留まらない。その剛直さが充分に増すと、そのまわりのしなやかな世界線は、曲がってしまう。もし、剛直な世界線が２本並んでいたら、互いに相手の世界線を曲げて、ねじれあう。
　質量の「慣性質量」としての側面が、世界線の曲がりにくさとして表れるとすれば、質量の「重力質量」としての側面は、他の世界線を曲げる性質として表れる。それは、質量の偏った集中が時空を歪ませるからだと一般相対性理論では解釈される。

　では、歪んだ時空は、数学的にはどのように把握されるのだろうか。
　さきほど、はさみとのりで作った歪んだ時空面の模型を取り出し、そこに定規を当てて、原点Ｏを囲むように三角形を描いてみよう。そして、その内角を測って和を求めてみよう。内角の和は３６０度より大きくなっているはずだ。これは歪んだ面の重要な特徴の一つである。今度は、原点Ｏを囲む直角三角形を描いて、辺の長さを測ってみよう。斜辺の２乗が残りの辺の２乗の和に等しいという三平方の（ピタゴラスの）定理は成り立っていないことが分かるはずだ。これも歪んだ空間の重要な特徴である。歪んだ空間ではユークリッドの幾何学は成立しなくなる。
　歪んだ空間を数学的に扱う際は、三平方の定理から乖離している度合いを考慮して、数式を組み上げていかなくてはならない。
　例えば、空間的隔たりの大きさ（ｄｓ）を表現するのに、ユークリッド空間では、
　(ｄｓ)²　＝　(ｄｘ)²　＋(ｄｙ)²　＋(ｄｚ)²　
ミンコフスキー時空では、
　(ｄｓ)²　＝　－(ｄｔ)²　＋(ｄｘ)²　＋(ｄｙ)²　＋(ｄｚ)²　
で、表現された。これは三平方の定理（およびその変形）そのものである。しかし、一般に歪んだ時空では、
(ｄｓ)²　 ＝ｇ_μν ｄｘ^μｄｘ^ν
となる。これは、
(ｄｓ)²　
＝ｇ₀₀ ｄｘ⁰ｄｘ⁰ ＋ｇ₀₁ ｄｘ⁰ｄｘ¹ ＋ｇ₀₂ ｄｘ⁰ｄｘ² ＋ｇ₀₃ ｄｘ⁰ｄｘ³
＋ｇ₁₀ ｄｘ¹ｄｘ⁰ ＋ｇ₁₁ ｄｘ¹ｄｘ¹ ＋ｇ₁₂ ｄｘ¹ｄｘ² ＋ｇ₁₃ ｄｘ¹ｄｘ³
＋ｇ₂₀ ｄｘ²ｄｘ⁰ ＋ｇ₂₁ ｄｘ²ｄｘ¹ ＋ｇ₂₂ ｄｘ²ｄｘ² ＋ｇ₂₃ ｄｘ²ｄｘ³
＋ｇ₃₀ ｄｘ³ｄｘ⁰ ＋ｇ₃₁ ｄｘ³ｄｘ¹ ＋ｇ₃₂ ｄｘ³ｄｘ² ＋ｇ₃₃ ｄｘ³ｄｘ³
の意味である。
　ここでは、ｄｔ，ｄｘ，ｄｙ，ｄｚという表現の変わりに、添え字を使って、ｄｘ⁰，ｄｘ¹，ｄｘ²，ｄｘ³という表現方法を取る。右上付きの添え字は階乗を意味しない。階乗は括弧を付ける。「　ｇ_μν ｄｘ^μｄｘ^ν　」という式のように、同じ添え字が左下と右上にあらわれたら、その組み合わせの分の和を取りなさいという縮約規則があって、一般相対性理論では、例えばこのような取り決めを設けて、複雑で長ったらしくなる数式を簡潔に表現することが多い。だが、不慣れな者には分かりづらい。
　ここで、係数を、ｇ₀₀＝－１、ｇ₁₁＝ｇ₂₂＝ｇ₃₃＝１、それ以外のｇ_μν（μ≠ν）は零、とすれば、ミンコフスキーの計量に一致する。（この特別な係数の組み合わせを、η_μνと表現することがある。）これらの係数ｇ_μνが、この特別係数η_μνから乖離していると、それは歪んだ時空での計量を表現するものになる。要は、単なる２乗の和ではないぞという部分が立ち現れてくるわけだ。この係数の組み合わせｇ_μνは、計量テンソルと呼ばれる。
　この時空の隔たり（計量）は、どんな座標系で測っても一定不変であるべきである。実際、ミンコフスキー計量は、座標変換であるローレンツ変換に対して不変に保たれる。だが、歪んだ時空は、座標系は曲線座標系であり、ローレンツ変換は成り立たない。一般の曲線座標系間の変換規則が求められる。そして、その変換は、時空の計量を不変に保たなくてはならない。

　では、時空の歪み具合そのもの（曲率）はどんな感じで定義されるのだろうか。今一度、時空面の模型を取り出してもらいたい。そこに、短めの線分を描いて、それと平行な線分をすぐ隣に描き、さらにそれと平行な線分を隣に描き、ということを、原点を一周する形で続けてみる。平らな平面なら、最初に描いた線分と最後の線分は平行な関係になっているはずだが、この歪んだ面では、平行でない方向を向いて戻ってくる。これも歪んだ時空間の重要な幾何学的特徴である。曲率はこんな特徴を利用して定義されたりする。
　座標系の座標軸は、その方向と、目盛のピッチを表す基底ベクトルで表現できる。この歪んだ時空面の模型では、右下と左上の部分の基底ベクトルと、左下と右上の部分とでは、異なる基底ベクトルになる。右下から左上に移動すれば、基底ベクトルが、直行系から斜交系に変化してしまう。実際は、こんな折れ線座標系は非現実的で、滑らかに変化していく曲線座標系になるわけで、これは基底ベクトルが徐々に変化していく座標系なのである。我々が通常馴染んでいる真直ぐなユークリッド空間、もしくはミンコフスキー時空間は、どこまで行っても、基底ベクトルは一定不変だ。ものさしは、不変であり、その中で対象の変化を考えればよい。しかし、この歪んだ時空間を扱う幾何学（リーマン幾何学という）では、基底ベクトルは場所や時間の関数なのだ。ものさしの向きや目盛幅が、どんどん変化していくところで、対象の変化を記述するという、まことにややこしいことをやってのけねばならない。

　ここまで書いてきて、ああ、やっと一般相対性理論の数学的記述の入り口地点にたどり着いたのかなという気がする。なんて書いたら気が滅入るかな。でも、事実そうなのだから仕方がない。私自身、滅入っているのだ。
　このあとも、いろいろ、概念的な下準備が数多く要求される。
　まず、曲線座標系は、斜交系を不可避的に含む。すると、直交系では区別する必要のなかった、ベクトルの反変成分と共変成分とかの話をして、ひしゃげた座標を扱えるようにしておかなくてはならない。
　そして、テンソルというベクトルを拡張したような線形写像形式について学ぶことが要求される。時空の曲率も質量（エネルギー・運動量）の密度も皆、この形式で表現される。こうすると、座標変換に対して、不変の式で書ける。そうしてさらに、基底ベクトルが変化していくような曲線座標系での微分幾何学を学ばなくてはならない。これが、大変なのだ。
　このへんのきっちりとした説明は、素人の私などが下手に手を出すべきではあるまい。しかるべき参考書が、専門的なものから入門的なものまで数多くでているので、気概の溢れた読者は、そちらを参考にしてもらいたい。
　ここでは、大いにはしょって、いきなり結論のアインシュタイン方程式を掲げてしまうことにする。

indexへ

　結局、重力場についての、アインシュタインの方程式は、以下のようになる。

Ｒ^μν　－ (1/2)ｇ^μν Ｒ ＝ κ Ｔ^μν　（ただし、κ＝８πＧ／ｃ⁴）

　歪んだ時空内のある一点（微小領域）において、上記の関係が成り立つと言っている。
　まず、右辺について。
　Ｔ^μν は、エネルギー・運動量テンソルとよばれているものである。（単位は質量の次元なので、４次元質量テンソルと言ってもいいかもしれない）　前に、世界線の４次元質量ベクトルというものを説明した。それの時間成分はエネルギー、空間成分は運動量に相当するものを表現していることを述べた。だが、線状のシンプルな構造ではない厚みのある構造をより厳密に考えるとこの４つの成分だけで、その場所（時空点近傍）の質量（エネルギー・運動量）事情は表現しきれない。「応力」の要件をも考慮しなくてはならない。ある方向、（ｘ^μ軸方向）について考えた場合、質量（エネルギーor運動量）成分の密度（その方向に伸縮される圧力）の他に、他の３つの時空軸方向にずれ込む力という合計４つの要因がある。それを、各々４つの時空軸方向について考えなくてはならない。それで、ベクトルよりも複雑なテンソルを用いて表現される。成分の数は、４×４の１６通りである。
　比例定数 κ の値は、地球付近のような弱くてシンプルな重力場においては、アインシュタインの方程式がニュートンの万有引力の法則と近似的に一致するようになること、という条件で求められた。Ｇは万有引力定数、ｃは光速である。
　
　次に、左辺について。
　ｇ^μνは、その時空点での計量テンソルである。時空点の隔たりがどう定義されるかに関わる係数群で、歪んでない時空の場合は、ミンコフスキー計量η^μνになる。（先ほど出てきたのと添え字の位置が上付か下付かで違っているけど、説明しだすと面倒なので、気にしないで欲しい。）
　Ｒは、スカラー曲率で、その時空点における歪み具合全般に対応した、一つの値である。
Ｒ^μν は、リッチのテンソルと呼ばれているもので、各々の成分は、その時空点における、各時空軸方向、並びに先ほど説明した応力要因に対応したそれぞれの曲がり具合を表現している。（偏微分形式）

　従って、この方程式は、各テンソルの成分ごとに合計１６個の方程式を表現している。ただ、例えば、μν＝1 2　のものとμν＝2 1 のもののようにμとνとを入れ替えたもの同士は、全く同じ方程式になるということが保証されているので（対称テンソル）、01 02 03 12 13 23 と同等になる、10 20 30 21 31 32 の６つの方程式は無視できる。よって、このアインシュタインの方程式は、１０個の連立方程式だと考えればよい。ただし、それぞれが、複雑な偏微分方程式であり、おいそれと解けるようなものではない。
　微分方程式というのは、限りなく点に近い微小な領域の構造がどうなっているかを表現したもので、それは普遍的な法則性についての思想を物語ることはできても、それだけではあまり実用に役立たない。ある程度大域的な範囲で、パラメータを与えたら、どこそこではどうなるかが言い当てられるような関数を手にしないと実用的ではない。しかし、このような関数（原始関数という）を無条件で求めるのは困難で、色々前提条件を設定した上で積分等の計算技術を駆使して求めていく。方程式が非線形だと（比例的でないと）大変難しい（らしい）。一般相対性理論の方程式は横綱級の難しさで、天才的な数学者でないと解けない（らしい）。
　有名なシュワルツシルツの解は、00 11 22 33 という対角成分以外は零になる、すなわち、ずれ込みの応力成分はないものとし、１点に質量が集中した球対称な静的な重力場という単純化の前提で、一般解（原始関数）を求めたものである。なんて書いたらすごい簡単そうに思われてしまいそうだが、とんでもない。少なくとも、私はお手上げの世界である。
　具体的な適用を考えるとたいへんややこしいのだが、まあ、一言で、この方程式について述べるならば、左辺の、歪んだ時空の曲率は、右辺の、質量（エネルギー・運動量）密度に比例しているという思想の表明なのである。比例定数κ＝８πＧ／ｃ⁴は、単位系の採用という地球的、人類的な偶然要因によって左右される値にすぎないのだから、つまるところ、この方程式は、時空の曲がり具合、すなわち質量の集まり具合だと言っているわけである。そして、時空の曲がり具合の激しいところほど、その時空の測地線（これはこれで厳密な方程式として定義される）の曲がりも激しくなり、（落ちまいとすれば）大いなる重力（慣性力）を感じとることになるわけだ。

indexへ

　以上、ざっと見てきたように、相対性理論は、結局、「力学」を「時空の幾何学」に置き換えてしまったわけである。
　事の発端は、アインシュタインの見出した数式に対して、彼の先生であるミンコフスキーが、これを幾何学的に表現すれば、こうなるね、と４次元時空表現を与えてしまったことである。当のアインシュタイン自身は、「そうかもしれないけど、そんな考え方は、ちょっとね」と言ったかどうか知らないが、当初この表現には拒否反応を示していたと伝え聞く。しかし、その後、重力の問題と取り組み始め、リーマン幾何学の活用を思い至る段階で、４次元時空は、アインシュタインの思想に積極的に取り込まれていく。リーマンら数学者たちにとって、この新しい幾何学は、単なる論理的可能性の追求でしかなかった。純粋に数学の世界だけのものと思われていたわけだが、アインシュタインは、現実の宇宙の表現手段に仕立ててしまった。

　さて、ここで、先にちょっと提起しておいた問題を考えてみたい。すなわち、
「世界線が曲がるのは、力がそこに働くから曲がるということなのだろうか？
それとも、曲がった世界線がそこに存在しているから、そこに力というものが認識されるということなのだろうか？」
という問題について。

　物体は、真直ぐに一定の速度で進むのが本来の姿である。それが曲がったり速さが変わったりするのは、なにか原因がなくてはならないはずだ、すなわち、原因たる「力」がそこに働いていなくてはならない。それが、ニュートン力学の世界観である。真直ぐなもの、不変なものは、説明不要で、曲がったもの変化するものは「力」で説明されるべきだという考え方だ。一般相対性理論の思想は、実はこの常識を崩したのである。重力場のあるところで落ち行く世界線、それは曲がっているけれど、歪んだ時空に素直に従っているにすぎない、説明されるべきは、曲がらないでいる地表にへばり付いている世界線の方なのだ、と。実際「力」（押し潰れないように踏ん張る斥力）が働いているのは、落ちないでいる方なのだ。
　しかし、それは力が働いていると言うよりは、存在が主張されていると表現したいような状態である。
　翻って、今度は平坦な宇宙空間について考えてみよう。今度は真直ぐな世界線は、真直ぐな時空に素直に従っている状態である。ここで、加速度系は曲がった世界線である。この場合、何故曲がるのか？
　誰かが引っ張る場合も考えられるが、それだと、その誰かは何故引っ張れるのかを問わなくてはならなくなる。ここでは、自立して加速していく現象を考える。典型的な事例は、やはり、ロケット噴射によって推進していくケースであろう。
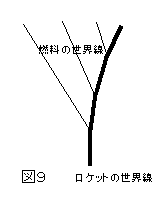　　なぜ、ロケットは、推進して行けるのだろうか。それは、燃料内部の静止質量を、燃焼という反応を通して、運動エネルギー的な質量に変換し、進行方向と逆方向に飛翔させ、それの反動で、進行方向に進むのである。これを、燃料－ロケット系全体の４次元構造で捉えると、ロケット内の燃料の部分が宇宙空間に広がって行き、ロケット本体は、少しカーブを描く世界線になるといった構造である。エネルギー・運動量（質量）保存の法則から、系全体のエネルギー・運動量（質量）が一定であるためには、ロケット本体は燃料とは逆方向に曲がっていないと、バランスしない。だから加速という現象が生じる。
　こう考えると、この現象の意味するところは、ロケットが加速して行くことというより、宇宙に拡散していく燃料－ロケット系が４次元時空内に存在していることというべきではないだろうか。ロケット本体だけでは自立した体系ではないのだから。
　注目したいことは、この全体系の観点からは、「力」というものが何かに働くという観念は表れないことである。あえて、この全体系から、ロケット本体の系を切り出した場合、その系は、力を受けて加速すると言える。しかし、この切り出しは恣意的な視点からの分析である。「力」が働いて、ロケットが加速するというよりも、この物質拡散系の一部分でしかないロケット本体系という視点において、「力」が働いているような現象が観測されるということでないだろうか。要は、加速運動の原因たる力というものを何かしらの実体として捉えるような考え方は、相対性理論にはそぐわないのではないかと私には思われる。
　従って、世界線が曲がるのは、力がそこに働くから曲がるということではなく、曲がった世界線がそこに存在しているから、そこに力というものが認識されると、相対性理論では解釈されるべきではないかと思うのである。
　そして、このことは、実在するのは４次元時空なのだ、という観点が正しければ、もはや決定的になるのではないだろうか。（先の二論文を、参照のこと。）
　では、量子力学の観点を付き合わせると、どうなのか。素粒子物理学では、「力」は、それを司る素粒子（例えば、電磁気力では電子、核力では中間子）の放出・吸収を通じて運動量が授受されることによって生じると説明される。（この粒子は波動的性格を併せ持っている。）これらの考え方が、相対性理論と矛盾しているわけではない。ファインマンのダイアログ等に示されるように、量子力学も特殊相対性理論の時空の中で語られる。相対性理論は、世界の、時間・空間・質量という量的側面の関係性を抽象化し理論化したものである。世界のより具体的な構造は、素粒子物理学のような別次元の理論で語るしかないのだ。だが、枠組みとしては、確固たるものを提供している関係にある。そう考えると、量子力学は、時空の具体構造に関わる理論と位置付けられる。つまり、素粒子のやりとりをする時空の存在として、「力」は説明されるわけで、実体化された力なるものはやはり表れない。

　我々は、何かの原因として、「力」という概念をよく使う。なにがしの力が働いて、こうなった、ああなったという言い方を大変好む。一般に「力」とは何を意味するのだろう。「力」という概念は何も、物理学に限って使われるわけではない。「経済力」とか、「軍事力」とか、「精神力」とか、「企画力」とかいろいろな使われ方をする。これらは、物理的な「力」に還元させることはできない。
　今、ここで、すべての「力」概念をあますことなく規定できるような一般的定義を与えようとは思っていない。それは、容易なことではないだろうし、本稿のテーマからもはずれるだろう。あくまで、ここで問題にしているのは、物理学が扱うところの「力」に限っている。
　しかし、そうは、言っても、いかなる「力」も時間と空間の内部で生じることである。その意味で、４次元時空内の存在なのであり、ここで考えたようなことと全く無縁でいられるかどうか。そこに、ある「力」が働いたからそうなった、ということではなく、そうなるようになっているから、我々はそこに「力」を認知するのだ、ということが、一般的に言えやしないか？ひょっとしたら、「力」というものを何がしかの実体として捉える考え方そのものが一般的に問われているのではないか？そんな気持ちを拭い去ることができないでいる。

indexへ

　一般相対性理論の「一般」とは、何を意味しているか。それは、慣性座標系に限らない加速度系、重力場系（曲線座標系）すべての座標系について、「一般的に」成立する法則について述べた理論であるということを表明している。つまり、座標系に対する一般性と理解されている。しかし、それだけに尽きることであろうか。
　ここでは、一般相対性理論における一般性の意味について、もう少し突っ込んで考えてみたいと思う。
　アインシュタインは、ある信念を持って、新しい物理学理論の構築に挑んだ。その信念とは、この宇宙は、単純で美しい法則性で語られるべきであるというものである。そして、達成されたアインシュタインの方程式は、その形は驚くほどにシンプルであり、美しくもある。
　だが、それの具体的な適用は、ということになると、眩暈がするほどに複雑だ。このギャップは一体何なんだろう。
　一方、ニュートンの万有引力の法則は、大変シンプルで美しい。そして分かりやすく、扱いやすい。もちろん、対象が複雑であれば、（例えば３体以上の天体が相互連関する様など）それの適用は難しくなる。万有引力の法則は、重力場ポテンシャルの考え方で、電磁場のように場の理論として微分方程式の形で書くこともできる。その場合、原理的にはどんな複雑な質量分布にも対応できる一般理論になる。ただ、一般解が見つかるかどうかは条件次第。通常は、摂動論のように、適用範囲を限定して近似計算をはかる。いずれにせよ、座標系は、絶対空間・絶対時間の考えを反映しているので、直線的で、不動のものである。一般相対性理論はその前提さえも崩して、座標軸のあり方までが時と場所の関数になってしまった。
　これは、シンプルさの一般性が、大きく後退した姿だとも言えないだろうか。一般相対性理論はケース・バイ・ケースに確定していかなくてはならない要素を大きく拡大してしまっているのである。
　ニュートン力学の世界観では、自然は数理的な世界が示す様に、きっかりと直線的なものこそが本来的姿であって、そうでないのはなにがしか理由があってのことという暗黙の前提があったように思う。それ故、慣性運動＝等速直線運動として考えられる。しかし、一般相対性理論の世界観では、所詮、世の中なんてのは、曲がったことだらけなんで、時空だって曲がっていて何の不思議があるだろう、といったもので、慣性運動＝時空の歪みに沿った運動として考えられる。物体は、方円の器に従う水のごとく、時空の歪みに従って落ちるのである。
　しかし、それを数理的に表現せねばならない。だが、数理は元来、直線的なものを好む。曲がったものは、微小区域に分割して、その範囲では直線的な構造として把握しておいて、連続的な変化を扱える論理である微積分学に基づいて、曲がったものの全体把握にアプローチするというまどろっこしいことをしなくてはならない。
　思うに、一般相対性理論とは、「時空具体性理論」と言えないだろうか。一般的に法則として言えることは、微小区域におけるかくも抽象的で、多くの要因を配慮しなくてはならないような関係のみであって、その構成要因はことごとく時と場所の関数なのである。ニュートン力学では時間と空間に対して、歴史性、地理性を考慮することなど、思いもよらぬことであった。だが、アインシュタインは、時間や空間も歴史的、地理的なものなのだと言い放ったのである。そしてその具体性は、質量分布によって示されるのだと。
　かくして、宇宙の歴史・地理は、時空の歴史・地理として把握される現代宇宙論の基礎が築かれたと言えるのではないだろうか。

indexへ

戻る