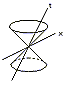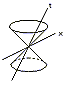Movement of the Minkowski space-time coordinates

Frame of reference A
Frame of reference B

move the Origin  change display Size
slope(velocity)    line of same time/same position

      interlocked
     c = velocity of A to B; v/c=
Browser that supports the canvas tag is required to view the graphics.
Try applet site.

[explanation]

  For understanding of the (special-)Relativity, it is indispensable to understand the space-time coordinates devised by H. Minkowski.
  But it is hard to understand it enough by only looking at static printed diagrams. Here, you can move the time axis, the origin or so on so that you can see the movement of space-time axes with feeling.
  Two red straight lines to cross obliquely show the world line of the light by this graph.
  A black straight line shows a time axis and a space axis. A line in the vertical direction with mouse sensibility is a time axis.
  A blue straight line shows a line of the same time in each coordinates. (line parallel with the space axis)
  A green straight line shows a line of the same spot in each coordinates. (line parallel with the time axis)

(Light Cone)   Actually, the space-time is four-dimensional, but here is showed two-dimensional space-time by reducing space to one dimension for simplicity. When the space is assumed as two dimensions, the space-time graph becomes a three-dimensional shape which has a curved surface boundary which is made by revolution of the world line of the light around the vertical axis. This curved surface is a shape that is like two cones standing opposite to each other in top and bottom. These cones are called a Light Cone.
  It is impossible for us to draw the actual four-dimensional spase-time which has three-dimensional space. We cannot handle it by not less than mathematical formal method. In the 4-D world, the circle (oval) of "the section" of the Light Cone is equivalent in the spherical surface (spheroid surface) of the Light Cone as super-solid.
  But, what is showed here is only reduced two-dimensional space-time diagram.

[USAGE]

  You can set up operational mode with the following controls and move the line of the graph.

"Frame of reference" Choice Radio Button

It prepares for A and B two frames of reference here. You can choose Radio Button Frame of reference A or Frame of reference B as an operational object.

"interlocked" Check Box

As for both coordinates, you can operate each single one, or operate them interlocked. When you want to take the interlocked mode, check the "interlock" check box.
The concrete motion in the interlocked mode is different by selection of operational object such as an origin, a time axis, or a simultaneous line. It will be mentioned in detail later.

Radio Buttons of Operational object

After A or B is chosen, you can choose from the following radio button which decide the operational object.

  • move the Orgin

    • The origin of the coordinate is moved to the position where mouse clicked.
      (interlocked mode)

    It is made to fix the distance between A and B's origin, and both coordinates move in parallel.
  • slope(velocity)

    •  You can change the slope of a time axis. This means a velocity in a frame of reference (for example, in rectangular coordinates). It is impossible to slant beyond the world line of the light. (It must be under the velocity of light.)
     The space axis changes its slope interlocked with the time axis (to keep the velocity of light).
      (interlocked mode)

      The slope of another axis can be interlocked under keeping the velocity between the frame of reference A and B. The rate of change of the slope will become slow according to approaching velocity of light. The relations between A and B are equal physically even if you don't choose rectangular coordinates. It is no more than difference of expressions.
  • line of same time/same position

    •   You can move the line paralleled against the space axis by your mouse. That line means the same time in the current frame of reference.
    And you also can move the line paralleled against the time axis by your mouse. That line means the same place in the current frame of reference.

      And you can move the same time (place) line under fixing the same place (time) line by the following operations.
          When the "T" is typed, you toggle the fixed mode of the same time line.
          When the "X" is typed, you toggle the fixed mode of the same place line.

     (You can see hyperbola line which is tangent to the line of the same time or the line of the same spot.
     It shows the locus of points which are equal time or are equal distance from the origin.
      (And, when the "H" is typed, base hyperbola yellow lines will become non-displayed or displayed.))

      (interlocked mode)

    Both in A or in B, the two lines of the same time will keep time equality from the origin (or to the origin). You can see that other's clocks are delayed each other.
    And both in A or in B, the two lines of the same spot will keep distance equality from the origin (or to the origin). You can see that other's measuring-rods are contracted each other.

  • change display Size

    • This is chosen when you want to change the range of the graph with a mouse.

    Selection Box of the Value of Light Speed

    You can change the slope of the world line of the light. Usually, it is set as "c = 1".( "c" means the speed of light) If the value of light speed (in other words, the value of ratio of distance-unit to time-unit) become larger, you will see it approaches to the Galilei translation's world. You will make sure by using this box.

    （Other Informations）
      You can put number directly to the text box of "the velocity of A to B".
        (But, it must be a real number which is bigger than -1.0, and is smaller than 1.0, by the unit of "c = 1".)

      You can change the display position of the numerical information by left-click with pushing a SHIFT key.
      When the "G" is typed, you toggle the display mode of the grid.
        ( Nothing → A only → B only → Both → )    the pitch is 50.


    [ About the Numerical Information ]


  • A-B distance in rectangular coordinates (t,x) = (###0, ###0)
         The numerical value which measured the interval of each origin of the coordinates A and B by a rectangular coordinates system.

  • A's origin coordinate on Ref. of B (t,x) = (###0.000,###0.000)
    The coordinates of the origin of the system A which is expressed by the system B.
           s*s = - t*t + x*x = ###0.000 (s=###0.000)
           space-time measure; (if this value is negative then A and B is positioned in timelike, if positive then in spacelike, if zero then lightlike.)


  • B's origin coordinate on Ref. of A (t,x) = (###0.000,###0.000)
    The coordinates of the origin of the system B which is expressed by the system A.
           s*s = - t*t + x*x = ###0.000 (s=###0.000)
           space-time measure; (the same value as the above case.)


  • A's velocity in rectangular coordinates = #0.000000000

    • The velocity of system A against the rectangular coordinates system.


  • B's velocity in rectangular coordinates = #0.000000000

    • The velocity of system B against the rectangular coordinates system.


  • A's velocity by Ref. of B = #0.000000000

    • The velocity of system A against the system B.


  • (each)  γ = #0.000000000    1/γ = #0.000000000

    • The value of  γ  ( = 1 / √(1 - v2) )  corresponding to each velocity (v);   and it's reciprocal.
       ( It means the rate of time delay.
           In this connection, it can be said as following;
           m0 * (γ - 1) = E / c2    m0:stationary mass ;  E: motion energy )


  • A's time = ###0.000      A's position = ###0.000

    • The time when the line of the same time in the A-system points it out; the position where the line of the same spot points it out.


  • B's time = ###0.000      B's position = ###0.000

    • The time when the line of the same time in the B-system points it out; the position where the line of the same spot points it out.





    • BACK