CHAPTER II    The Problems of Continuity and Contradiction

2. Achilles and the Tortoise Based on the Principle of Relativity

   Just as in Zeno's era, Aristotelēs did not recognize the law of inertia. The belief was that an object would stop moving unless any force was added to it. However, Galileo Galilei changed this thinking. If no force is added to an object, the object gets into uniform linear motion. Einstein also followed this rule.
   Now, let's think about Zeno's paradoxes involving Achilles and the tortoise from this modern perspective. In this simulation, Achilles, the tortoise and Dr. Zeno, who observes them, are put in space to exclude consideration of complicated factors, such as friction against the ground.


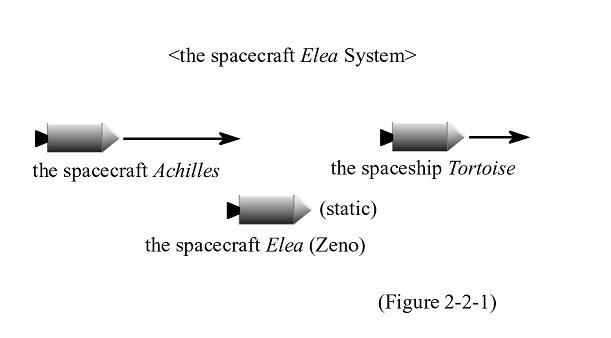
   Astronaut Tortoise is traveling slowly from the earth aboard the spaceship Tortoise in the direction of Sirius. His spaceship does not accelerate. Astronaut Achilles is chasing the Tortoise aboard the spacecraft Achilles from far behind. This spaceship is not accelerating either, but is moving from the earth more quickly than the spaceship Tortoise. Dr. Zeno is observing these two spaceships aboard the spacecraft Elea. His spaceship is almost static in relation to the earth. Dr. Zeno's being aboard the spacecraft is intended to remove complicated conditions, such as the earth's rotation and yearly trip around the sun. In this scenario, the earth is excluded. Just consider the three spaceships moving (or remaining static) on a straight line in the same direction. Dr. Zeno thinks as follows. When the spacecraft Achilles reaches a certain spot where the spaceship Tortoise existed at a certain point in time, the spaceship Tortoise must be flying ahead. When the spacecraft Achilles moves forward, the spaceship Tortoise must be again ahead of it. The endless repetition of this chase makes it impossible for the spacecraft Achilles to catch up with the spaceship Tortoise.
   An important point here is that only the coordinate system of the spacecraft Elea is not absolute. The movement observation results based on any other inertial system of coordinates have equal significance. This is the physical principle of relativity that has been consistent since Galileo.
   In response to this situation, Astronaut Achilles, who is aboard the spacecraft Achilles, judges that the spacecraft Elea is moving backward and that the spaceship Tortoise is approaching him, while he is of course static (See Figure 2-2-2). In the meantime, Astronaut Tortoise, who is aboard the spaceship Tortoise, thinks that the spacecraft Elea is going away but that the spacecraft Achilles is getting close (See Figure 2-2-3). That is just the way it is. From the perspective of someone in a static coordinate system, Zeno's paradoxes do not occur. Or if the spacecraft Elea is traveling at the same velocity as the Achilles or the Tortoise, Dr. Zeno will not face any paradox. The question becomes what things will be like if the spacecraft Elea is traveling away from the earth quicker than the spacecraft Achilles. Then, the situation in which the spaceship Tortoise chases the Achilles will occur. This enables the paradox, but the spaceship Tortoise will never be able to catch up with the Achilles (See Figure 2-2-4). That is, the emergence of paradoxes depends on a coordinate system as a standard. A paradox can sometimes appear in an opposite form. This suggests that Zeno's paradox about Achilles and the Tortoise is inconsistent in accordance with coordinate transformation. Physics regards consistent relationships and nature regardless of coordinate transformation as essential. The paradox of the scenario depends on an observer's system of coordinates and is regarded as inessential. The question then becomes what is universally consistent in relationship to coordinate transformation. In this simulation, the distance between the Achilles and the Tortoise and its changes are universally conserved. The fact that the distance between the spaceships Achilles and Tortoise gradually contracts can be observed in any coordinate system. (In the case of the theory of relativity, the measurement timing of the distance between the Achilles and the Tortoise somewhat differs depending on a coordinate system, but the distance values are assured to be consistent in any coordinate system.)


   The subject of catching up and overtaking concerning Achilles and the Tortoise can be argued only when referring to their distance. Aristotelēs refuted this paradox by mentioning distance: "Achilles can catch up with the tortoise on the basis of the assumption allowing them to pass through the limited distance 'during limited time.'" Essentially, each actor's positioning can be exactly defined by the concept of distance.
   In Zeno's paradoxes about Achilles and the Tortoise, space is just an aggregation of spots and time is just an aggregation of certain points in time. Only order relations such as anteroposterior relation are defined for two spots or two points in time, while distance and time intervals are not clearly defined. In this context, space and time are just simple aggregations of points. However, for this type of aggregation, point distance cannot be mentioned. Modern mathematics defines points as a vector expressed in the form of a coordinate system when it deals with physical concepts of space and space-time, and defines the vector space by using abstract algebra's calculation methods as in the case of the theory of groups. Modern mathematics also defines the metric vector space by way of an inner product. With regard to distance (norms and metric), the definition is the function obtained from coordinates of two points following a particular rule. (Refer to mathematical texts for detailed explanations.) That is, modern mathematics shows that unless you define space as a well-structured aggregation of points, you cannot obtain space (space-time), in which kinematics can be developed. You cannot describe distance by just mentioning an aggregation of points.
   An important point is how the distance between Achilles and the tortoise changes. If the distance gradually shrinks, Achilles will catch up and overtake the tortoise. If there are no changes in the distance, Achilles will never be able to catch up with the tortoise because they are running at the same velocity. If the distance increases, the tortoise will get farther ahead of Achilles.
   In addition, also significant is if the changes in the distance are consistent. If Achilles gets closer to the tortoise in the beginning but the distance gradually becomes larger due to Achilles' slowing down (the case in which Achilles's pace slows down due to his lack of stamina or he runs in the opposite direction), he cannot catch up with the tortoise. This is exceedingly natural. If you consider things from the vantage point of the changes in the distance, you will not find anything paradoxical.
   Zeno's paradoxes about Achilles and the Tortoise have no erroneous elements in logic. Even in the case where the distance between Achilles and the tortoise decreases, the logic is infinitely correct just before the distance between them reaches 0. (Of course, this is based on the assumption that space and time can be divided without any limit.) This reasoning is a mathematical case in which the distance can be dealt with as an infinite series that converges on a particular value.)
   If space and time are just aggregations of spots and certain points in time and are not defined in terms of the metric space, they cannot be handled from the perspective of an infinite geometric series. In that scenario, it would be appropriate to understand that Zeno's paradoxes about Achilles and the Tortoise implicitly hints at the importance of the metric attributes of space and time.
   As noted above, Zeno's paradox about Achilles and the Tortoise can be completely resolved by handling it as a matter of the changes in the distance between them. Doing so has resolved the problem.

Back　　　 Prev　　　 Next