A PHILOSOPHY OF THE FOUR-DIMENSIONAL SPACE-TIME
The Worldview of Relative Simultaneity (MURAYAMA Akira)
CHAPTER I
Relativity and Four-dimensional spacetime
[The First half] ---- Outlining the Theory of Relativity ----5. The General Theory of Relativity and the Distorted Space-time
Minkowski was a mathematics teacher when Einstein was a student at the Swiss Federal Institute of Technology Zurich. In the beginning, Einstein was not much interested in this geometric representation that his instructor presented. Einstein, however, gradually became committed to addressing the concept of four-dimensional space-time and went deeper into the geometrical representation of mechanics than Minkowski. The primary motive for Einstein's interest in Minkowski's space-time beyond a merely mathematical motivation was to explore the subject of gravitation.
He focused particular attention on the double meanings of "mass." More specifically, "inertial mass," an indicator of the resistance of an object to acceleration, and "gravitational mass," the level of universal gravitation, are exactly proportional (within experimental error), though entirely different concepts. This has been demonstrated by Roland Eotvos's (1848-1919) high-precision experiments. Among many physicists interested in this issue, Einstein pursued it with insistence.
Einstein's thinking was that of a universal cosmopolitan. More specifically, his argument was based on the assumption that "zero-gravity condition" was the fundamental state of nature. On the earth, all objects move in accordance with the force of gravity in proportion to mass (the resistance to acceleration) working toward the center of the earth, which occurs only under the special environment of the earth. On the moon, objects with the same mass experience a different force. Furthermore the same mass will experience a different force if the distance from the center of the earth/moon is changed. In free space, far from massive bodies, gravity may be neglected and the mass of objects is only the amount of acceleration resistance (coefficient of inertia). For most of the universe, this state of weightlessness is quite common. When Einstein presented the theory of relativity, spacecraft did not yet exist and airplanes had just been invented. Then the most suitable device imaginable for simulating a state of zero-gravity was an elevator with cut cables. In fact, he imagined a situation where a person was in the elevator with cut cables to perform thought experiments. However, now that we live in a more enlightened condition in the twenty-first century, just think about this subject with a focus on outer space conditions.
Imagine a situation in which you accelerate a spacecraft in a condition of zero-gravity. In this situation, all objects in the craft are pulled in the opposite direction of the acceleration in proportion to their mass. This is the so-called inertial force, which we usually experience for a jackrabbit start or the sudden stop of a vehicle. Newtonian dynamics interprets it as a nominal force rather than real force.
Suppose that a space vessel accidentally approaches near a massive celestial body during its course and the pull toward that body becomes significant. This is called "free fall." Even in this free fall, the state of the inside of the spacecraft remains weightless. Newtonian dynamics believes that gravity is equally at work for all objects in proportion to their mass and that they accelerate toward the celestial body, which makes the spacecraft appear to be in a zero-gravity condition.
Now, imagine that the spacecraft tries to keep itself from falling by accelerating its rocket booster. Then, all things in the vessel begin to fall toward the celestial body. With regard to this phenomenon, Newtonian dynamics explains that the force on the things is gravity. However, from the spacecraft standpoint, the cause of the phenomenon of things falling by the boost of the rocket cannot be distinguished between an inertial force when a massive body does not exist near the space and gravity when the body exists near the space. Einstein called this the equivalence principle. That is, he noted that, empirically, inertial mass and gravitational mass are completely indistinguishable and equivalent and formulated that fact as a principle. That is, inertia force and gravity are indistinguishable. In our example, the force on the spacecraft when it travels away from celestial bodies by igniting its rocket booster is comprised of gravity as real power and inertial force as nominal power, but the equivalence principle denies the necessity of this distinction.
Einstein simply thought that a system of coordinates without any inertial force observed is an inertial system. More specifically, the system is not affected by any acceleration. Accordingly a system in which uniform linear motion works in free space and a system in which objects free fall toward massive bodies are both inertial systems. In both cases, no 'nominal' inertial force is apparent. However, the movements in both cases are clearly different from the reference frame of a distant observer. In one case the spacecraft continues to travel uniformly, whereas in the other, it accelerates toward the celestial body (or enters a rotational trajectory).
Einstein explained the two phenomena in terms of the distortion of space-time. In fact, the free fall system and the uniform linear motion system can be equivalent only within narrow limits in space-time. Wider-perspective examinations occasionally clarify delicate differences. Objects under the influence of gravitation move toward the center of massive bodies. Mutually distant objects freely falling toward the center of a celestial body will also approach each other. However, if the objects are at different distances their acceleration forces will differ in which case the distance between the two objects may become greater as they fall toward the celestial body. Objects are compressed horizontally and stretched vertically by gravitational gradients. (This is called tidal action.) The free fall system globally differs in its acceleration direction and magnitude.
The above-noted points can be approached by Newtonian dynamics, but the non-uniformity of time should be pointed out from the viewpoint of the theory of relativity. That is, in the free fall system (although it is a form of the inertial system) objects gradually accelerate toward celestial bodies. A system of different velocity differs in simultaneity. Space-time cross sections representing the same time (isotemporal surfaces) become more oblique as objects approach celestial bodies. In addition, unit time becomes longer, which means that time progresses in a different way. These differences are small at large distances from celestial bodies and larger at shorter distances. That is, the unit of time varies inversely as the strength of the gravitational field.
The accelerating system presents a similar world line to that of an object in free fall toward a celestial body. In this case, simultaneity gradually changes and Newtonian dynamics cannot explain this point. However, unlike the free fall system, in the case of the accelerating system, inertial force works for all objects as it resists the accelerating force. (See Figure 1-5-1.)
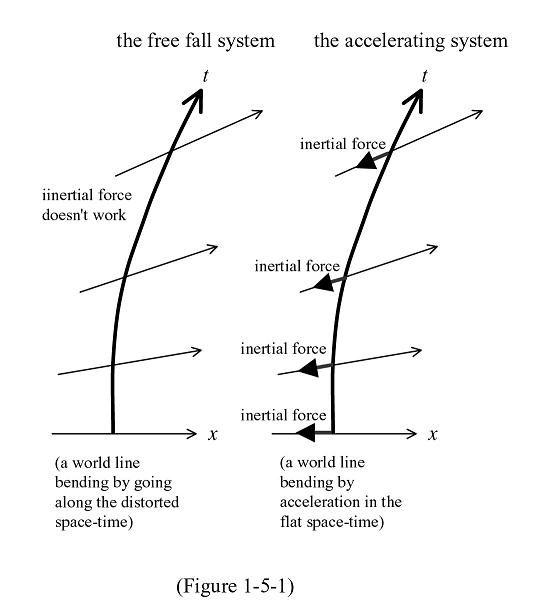
The reasoning for Newtonian dynamics suggests that in the free fall system, inertial force produced by acceleration (that is, the force of the ground on the sole of my foot) and universal gravitation happen to balance and counteract each other. However, Einstein was not comfortable with this interpretation. He thought that objects followed straight world lines in space-time in the free fall system and that the bending of their course was due to the distortion and curvature of space-time itself.
For example, if you walk straight along the earth surface, you will travel around the earth and come back to where you started because the surface is spherical, an example of a curved two-dimensional space. It is possible to expand this idea into a three- or four-dimensional space-time, although we cannot visualize it. Mathematically, although exceedingly complicated, this is quite possible.
Such mathematical models were studied by Karl Friedrich Gauss (1777-1855), Nikolai Ivanovich Lobachevskii (1792-1856) and Georg Friedrich Bernhard Riemann (1826-1866). Their models were based on non-Euclidean geometrical theories denying the parallel postulate of Euclidean geometry (there can be only one straight line through a point and parallel to another straight line). Einstein approached the new mathematical model with the help of his friend, Marcel Grossmann (1878-1936).
The parallel postulate of Euclidean geometry underlies the Pythagorean theorem. Therefore, a denial of the parallel postulate means a denial of the Pythagorean theorem. Drawing a right-angled triangle on a curved surface and calculating after measuring the lengths of its sides demonstrates that the Pythagorean theorem does not work. A curved surface is the stage for non-Euclidean geometry. As we saw earlier, the Pythagorean theorem is used to define the distance between two points in space given an orthogonal reference frame. The definition of Minkowski's space-time interval represents a minor modification and expansion of the Pythagorean theorem. In general the way to define the distance of a distorted space-time interval is more complicated. Riemann noted a particularly simplified case of largely complicated non-Euclidean geometry and discovered that the case was in fact simple Euclidean geometry.
Non-Euclidean geometry was thought a logical invention by mathematicians having nothing to do with the space and time of common experience. It was thought that space and time in Newtonian dynamics were like a homogeneous frame that could always be described with straight-line grids as on graph paper. Space and time were not treated as physical entities, but if you sit back and think about real things existing in the natural environment, you will surely know that such extremely precise things were just products of our imagination or artificially-crafted objects. Generally, many natural things are rugged or rough-surfaced and distorted or twisted. Few things are sharply flat and straight.
Einstein had already moved to handle space and time as physical subjects in the special theory of relativity. His approach was not based on a transcendental form of abstract recognition but on the assumption that space and time (space-time) were specific physical subjects like earth's surface. It was natural to suspect that they were not always purely straight.
Although I will not give detailed explanations of how things went, Einstein focused on Minkowski's concept of space-time as a linear base. That is, Minkowski's version of space-time was not at all distorted but was ideally linearly shaped. Based on this model, he noted that the difference in space-time curvature depended on whether mass (including energy and momentum proved to be equal to the mass) is localized or widely dispersed. In addition, he also set up an equation on the basis of the hypothesis that the density of mass and energy at a certain point of space-time is in proportion to the curvature (described by a four-dimensional mathematical tensor) of space-time at that point. Proportionality constants were specified on the assumption that under comparatively simple conditions where Newtonian dynamics can be established, the equation must come near to the law of universal gravitation. This is Einstein's equation for the gravitational field that constitutes the core of the general theory of relativity. The contents of this equation take the form of complicated simultaneous partial differential equations, but Einstein's unique ellipsis notations made the equation appear quite simple and beautiful. He had the fundamental belief that natural laws should be simple and beautiful. He kept to his strict principle in this case and took dozens of years to elaborate the simple and beautiful equation based on Minkowski space-time after the launch of the special theory of relativity.
In this generalized new geometrical field, a world line in inertial motion is not always a straight line and can be thought of as a curve connecting points of space-time in the longest elapsed time. This is called a "geodesic line." In the case of a spherical surface, an arc of a great circle constitutes a geodesic line. There the line is the shortest course, but the world line in space-time based on the Minkowski metric describes the longest elapsed time route. Obtaining the equation of this geodesic line is a major challenge for the study of dynamics in general gravitational fields.
The theory of relativity that had been presented initially was considered a special theory that exclusively worked in a particular system of coordinates (observer) for uniform linear motion in a state of zero gravity under certain linearly simplified conditions. That is why it was called the special theory of relativity. In contrast, the new theory compatible with all the system of coordinates including gravitating and accelerated systems of coordinates under the influence of gravitational fields was called the general theory of relativity.
According to the general theory of relativity, gravity and inertial force are the same and gravitational forces that we feel in our daily lives can be interpreted as the inertial force generated by the earth surface's skyward accelerating force to push our bodies upward. As a matter of fact, the distortion of space-time causes this phenomenon to occur without the earth swelling at an accelerated rate. The true nature of gravity we feel on the earth is the inertial force that the earth surface produces to prevent the "inertial motion" of free fall (against the geodesic line) in accordance with the twist of space-time. We are just constantly being pushed by the ground, not pulled by a distant action called universal gravitation. Actually the earth surface contacts us in the direction of pushing us upward, not the direction of pulling us toward the center of the globe.
No doubt it is quite natural that the distortion of space-time around the earth surface is a completely unfamiliar concept to most of us. Now, focus on the comparison of it with our physical size. The spatial distortion is a subject on a global scale. Our physical size is extremely small in comparison with it. Now think about the scale of the time unit. We usually think of one second as a small time interval because we can only do or think about a limited number of things within one second. In contrast, it is difficult for us to feel one year (currently elapsing year instead of past year) as a short period. We can do and consider many things during that period of time.
The speed of light is felt as staggeringly fast because we perceive the time interval (a second) in which the light travels 300,000 kilometers as a very short moment and the spatial scale as very large. If we could feel this moment (one second) as a long time (a very agile thinking and acting ability), we might experience the effects of the theory of relativity in our daily lives.
Now, let us return to the distortion of space-time. Around the earth surface it is quite small according to a unit system in which the speed of light is referred to as 1. It is almost straight. In fact, we are so insensitive to the passage of time that we perceive the speed of light as exceedingly fast and regard a small level of distortion as rather large. That is, we feel that an object breaks away from uniform linear motion into a free fall instantly. Our comparatively small body size makes us insensitive to the spatial distortion of space-time but our extremely dull sense of time passage makes us sensitive to the time distortion of space-time. This imbalance may prevent us from comfortably perceiving the distortion of space-time
Unlike many other physical theories, the general theory of relativity was not closely devised because it involved observations that cannot be resolved by conventional methods. The theory was a mathematical form of speculative philosophy based on Einstein's understanding of gravitation. However elegant the theory might seem to be, it was just a hypothesis by itself. It had to agree with observational facts to gain credit and authority as a physical theory. However, gravitational phenomena that can be observed in our everyday experience show similar results by both Newtonian dynamics and the general theory of relativity. A key opportunity to test the theory was provided by the movement of Mercury's perihelion. Newtonian dynamics could not explain this phenomenon, but strict measurement and the general theory of relativity proved to accurately describe the phenomenon. In addition, the general theory of relativity holds that the course of light progress also bends in strong gravitational fields. The theory on the refraction of a ray of light by gravity did not exclusively belong to the general theory of relativity, but Sir Arthur Stanley Eddington's (1882-1944) observations at solar eclipse in 1919 demonstrated that the bending of the sunlight was almost the same as predictions based on the general theory of relativity, with only a small margin of error. Many other facts support the validity of the general theory of relativity, and currently the theory is also applied to the precision improvement of the Global Positioning System (GPS). The general theory of relativity constitutes the very foundation for modern astrophysical theories, such as the Big Bang.
Black holes have become well-known only by name. The name is derived from the ultra-high-density state of mass in which there occur gravitational fields so strong that even light cannot emerge from them. The general theory of relativity suggests that time is also in an ultimate state. Cutting-edge modern physics focuses on the center of the black hole and the very first moment of the Big Bang. Even the general theory of relativity has not provided sufficient levels of solutions to these subjects in an ultra-high-density state. Conversely, with the exception of these extraordinarily difficult challenges, the general theory of relativity and quantum mechanics constitute the core of modern physics, as a comprehensive theory capable of treating every subject. (The integration of the two major theories has not been successfully achieved.) Additionally, a new attempt to tackle higher-dimensional subjects of space-time is under way in quest of a more comprehensive set of theories. Those efforts are based on ideas such as the relativity of simultaneity and the distortion of space-time that the theory of relativity has established. (The theoretical introduction of higher-dimensional concepts of space and time does not mean a denial of the one-dimensional time and three-dimensional space in our macro-level recognition of the universe.)
Copernicus and Galileo discovered the relativity of equipositionality and Einstein discovered the relativity of simultaneity. As a result of these discoveries the developmental history of physics from early modern times should be comprehensively considered based on this broader view that "here" or "now" is not always absolute.