A PHILOSOPHY OF THE FOUR-DIMENSIONAL SPACE-TIME
The Worldview of Relative Simultaneity (MURAYAMA Akira)
CHAPTER I
Relativity and Four-dimensional spacetime
[The First half] ---- Outlining the Theory of Relativity ----4. Minkowski's Four-Dimensional Space-Time
In the previous section, I presented two seemingly contradictory ideas, that (1) B's clock runs slowly from A's vantage point, and A's clock runs slowly from B's vantage point; and (2) B's scale contracts from A's vantage point, and A's scale contracts from B's vantage point. In fact, I declared these statements to be correct, despite their seeming contradiction, because if one's perspective shifts from a moving system of coordinates to a static one, or vice versa, the logic based on the principle of light speed invariance works. Some are likely convinced by my argument thus far. However, others may demand further explanation.
Time, in particular, functions as the very foundation for logical thinking. When human beings examine the logical authenticity of a matter, they typically consider the issue on the basis of the concept of simultaneity. The above-mentioned proposition, that B's clock runs slowly from A's vantage point, and A's clock runs slowly from B's vantage point, is obviously contradictory using the common frame of reference of simultaneity. However, the proposition does not present any contradiction because the notions of from A's vantage point and from B's vantage point are not actually based upon the commonly held form of simultaneity. Nevertheless, this does not mean that the incident described occurs in a totally different time frame. More specifically, the example wherein A's clock runs slowly one day and B's clock runs slowly on another day does not present itself. Rather, the proposition as stated is based on judging the same phenomenon in different systems of coordinates as well as on the assumption that the origin of the clocks' unit time is the same time (and at the same location). However, when the clocks' unit time ends, their positions differ. According to this reasoning, the judgment of simultaneity inevitably depends on a system of coordinates. In other words, it has a close association with the relativity of simultaneity. My point here is that time dilation and scale contraction should not be considered independently of the relativity of simultaneity. Minkowski's space-time diagram is a clear-cut illustration of this theory.
One example of a space-time diagram is a diagram of train, where a linear illustration shows the train's position along a horizontal axis line and the train's time on a vertical axis. This line showing the transition of moving points is referred to as a world line in physics. The direction of inclination of this line indicates the direction in which an object is moving. The larger the inclination is in relation to the time axis, the faster that object is traveling. The distance between the origin and another specific point along the same time line represents actual length of time. As the line becomes more oblique, it appears to be longer, when in actuality the time length remains the same.
Figure 1-4-1 illustrates the visions of space-time held both before and after the advent of the theory of relativity. In the space-time vision before the advent of the theory of relativity, the time axis was likely to slant, while the space axis was not. That is, the belief was that time progresses commonly in all systems of coordinates, thus underpinning the conventional worldview that time is consistent for every vehicle.
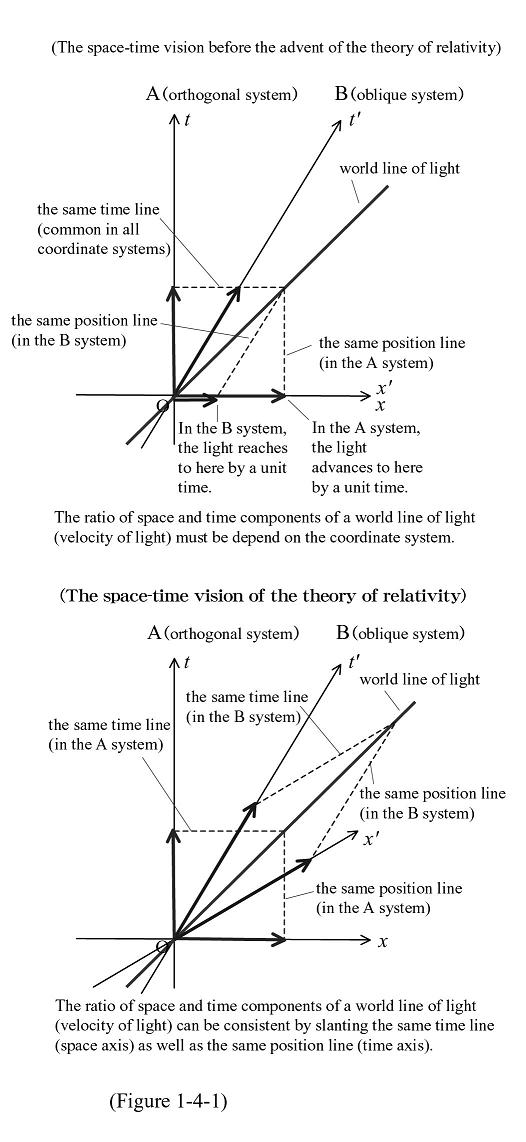
However, it was impossible to express the principle of light speed invariance through this space-time diagram. Light's progress, or at least a point of light's progress, could be expressed as a tilted straight line, a world line of light, but it was impossible that the speed of light would be consistent in every system of coordinates. However, if the space axis could be slanted as it is in the case of a time axis according to a system of coordinates, as the below figure illustrates, then the principle of light speed invariance could also be established.
Figure 1-4-1 illustrates that the space axis can be slanted such that the ratio of space and time components measuring the slope of a world line of light (i.e., the speed of light) will be consistent in accordance with the slanting of the time axis. The light speed invariance is then predicated upon the slanting of the space axis concerning space-time.
The slanting of the space axis represents the relativity of simultaneity, which is dependent upon a system of coordinates. This is because the space axis is a linear form of dots connecting points from the same time. In this way, the relativity of simultaneity is expressed as the slanting of the space axis in the space-time diagram.
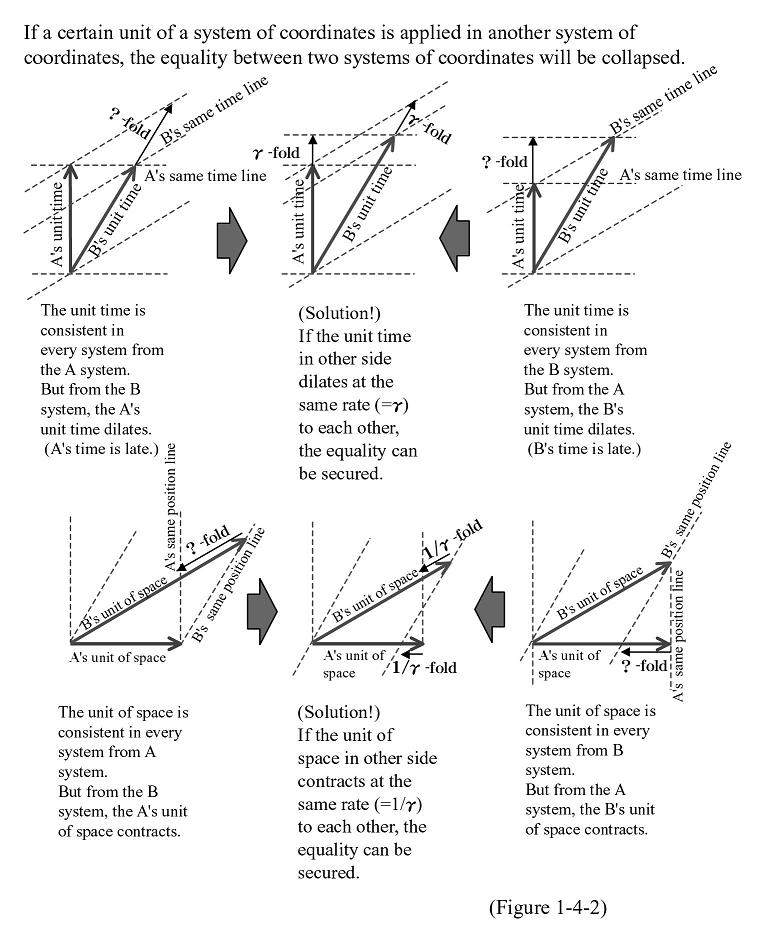
Next, this study addresses the issue of time length on the basis of Figure 1-4-2.
Think of a situation in which the unit time of a system of coordinates (for example, the system of coordinates expressed as an orthogonal system-the A system in the figure) is consistent in every system of coordinates. Thus, with regard to the orthogonal time length equal to the unit time in another system of coordinates (the system of coordinates expressed as an oblique system-the B system in the figure), the time prior to the end of the unit time in an orthogonal system corresponds to the end timing of the unit time judged in accordance with an oblique system due to the slanting line of the same time. This means that the time in an orthogonal system is late when measured from the vantage point of an oblique system. Conversely, if we suppose that the unit time in an oblique system is consistent in every system of coordinates, then the unit time measured from the vantage point in an orthogonal system is shorter than the unit time in an oblique system. This indicates that the time in an oblique system is late when measured from the vantage point of an orthogonal system.
The difference between orthogonal and oblique systems is merely a matter of how to express them; both are essentially equal. If you express a form of an oblique system as an orthogonal one, the former orthogonal system can be expressed as an oblique system that slants in the opposite direction. Of course, both systems can also be expressed as oblique ones. Therefore, it is incorrect to regard a particular unit time based on a particular system of coordinates as the special criteria in the entire universe. The only way to secure equality between two systems of coordinates is to highlight the recognition that the one's unit time is late at the same rate to each other. This means that the lines representing the same time as the end of both systems' unit time crosses in between the time axis of both systems. The rate of dilation can be obtained by the function of speed between systems of coordinates, the above-referenced γ.
This argument also works in the case of space. The above-mentioned figure is based on the unit system in which the speed of light shows a numerical value of precisely one. For instance, if seconds are employed as the unit of time, the unit of space is light seconds (one 300 millionth of a meter). This unit system displays as a symmetrical graph on the axis of a world line of light. Here, again, if you try to apply the unit of space to every system of coordinates on the basis of a particular system of coordinates, similar contradictions to the ones noted above will arise. After all, as the figure illustrates, to secure equality between two systems of coordinates, it is necessary to consider the assumption that there is an identical rate of expansion in their unit distance. The lines that represent points away from the origin by the margin of the unit distance cross in between the time axis of the two systems of coordinates. When describing the structure and condition of a specific thing, we usually focus upon a certain point in time. It is unusual to use images that link different points in time. Therefore, distances should be approached on the basis of segments using the same time line. This approach will demonstrate that the other's unit distance contracts at the same rate. Such a contraction rate is represented by 1/γ.
As a matter of fact, this graph facilitates the establishment of the Lorentz transformations. This formula is a numerical representation of the fact that position differs from the origin in accordance with time gaps (the relativity of equipositionality), and time differs from the origin in accordance with distance gaps (the relativity of simultaneity) with the γ-fold effect of the unit. If you set and solves an equation based on the assumption that inverse transformation is expressed in the form of the inverse sign of the speed between systems of coordinates, then the result is obtaining the function γ as it represents the expanding rate of unit length and establishes a transformation equation. (See below for details.)
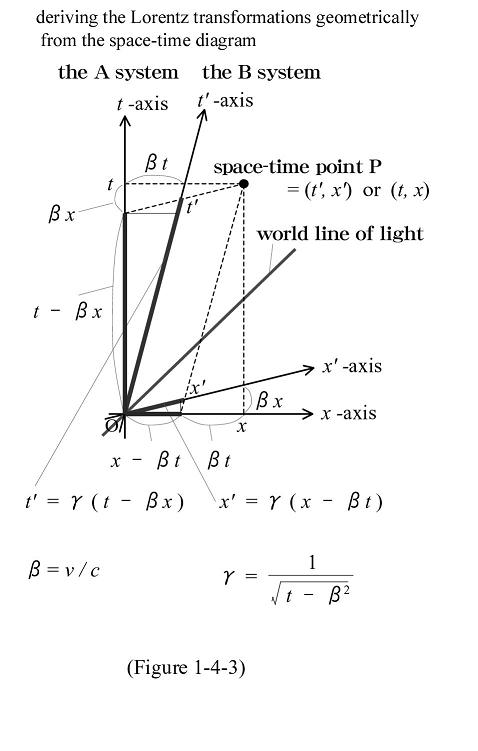
<The unit system is based upon a light velocity of the number one. β = v/c represents the speed between systems of coordinates on the unit system and its values range from negative one to positive one.>
With regard to the coordinate transformation from System A (t, x) to System B (t', x'), the formula (t - βx), one that is not used in the Galileo transformation model, is now used because time lag results when the position drifts away as a result of the effect of the relativity of simultaneity. In addition, the γ-fold effect is applied, thereby creating the following equation:
t' = γ(t - βx) ……(1)
Needless to say, the space coordinate's positioning changes along with the passage of time and (x - βx), which is the same formula as the Galileo transformation model, comes into consideration. However, the slanting of the space axis creates the γ-fold effect and the following equation results:
x' = γ(x - βt) ……(2)
In the case of the coordinate transformation from System B (t', x') to System A (t, x), and based on the assumption that inertial systems of coordinates are on an equal footing, a focus on the inverse sign of β, or the speed between systems of coordinates, leads to the following two equations:
t = γ(t' + βx') ……(3)
x = γ(x' + βt') ……(4)
If equations (3) and (4) are substituted for equation (1) or (2), γ can then be expressed in the form of the following function:
As these descriptions suggest, basic concepts in the special theory of relativity, such as the relativity of simultaneity, time dilation, length contraction and Lorentz transformations, can be clearly expressed by explaining them geometrically with the space-time diagram.
I have thus far intentionally chosen the expression "judging from A" and avoided using the expression "seen from A's standpoint." The act of "seeing" is a physical process and particularly if you try to see an object far away, some time is required for the information to be transferred even at the speed of light. Therefore two events that have happened simultaneously cannot be seen simultaneously and what can be seen simultaneously cannot be assumed to have happened simultaneously. Judgments on the simultaneity of two events depend on the information transfer process. The theory of relativity suggests that judgments are objectively different in different systems of coordinates. Much emphasis should be placed on this point because it can be easily misunderstood. The space-time diagram is of great help in avoiding this kind of misunderstanding.
Thus far I have confined attention to the concept of one-dimensional space, but space is actually three-dimensional. Accordingly space-time constitutes a four-dimensional structure, obtained by adding one-dimension of time to the three space dimensions. This four-dimensional space-time diagram is called a Minkowski space-time diagram after the mathematician Hermann Minkowski (1864-1909) who postulated its use in connection with the theory of relativity.
Four-dimensional space is beyond our abilities of perception, however mathematical representations of space are not subject to this limitation. The laws of mathematics remain valid, and formally infinite dimensional expansion is possible, as mathematical representations of space has a formal system.
To aid your visualization, we often reduce three-dimensional space to one or two dimensions and represent them graphically by allocating time to the vacant space dimension. Figure 1-4-4 illustrates one-dimensional space and two-dimensional space.
The three-dimensional space-time diagram is comprised of two cones facing each other, sharing the origin at their tips and taking the world line of light as a generating line. In this diagram, space-time is segmented into three realms: past, present and future. The cones are called light cones. Equal-time planes through them cut cross sections that are circular or elliptical in shape as the system of coordinates is orthogonal or oblique, respectively, although the difference in shape is only expressional. In the case of the four-dimensional space-time diagram, the circle or ellipse becomes spherical (or spheroid) spreading from a certain point, but it is difficult to imagine.
There are two light cones: one on the future side and the other on the past side. The inside of the future light cone is called the "future time-like region" and the inside of the past light cone is called "past time-like region." The outside of these two light cones is called the "space-like region" and is inaccessible to us. The space-like region of the two-dimensional space-time diagram is divided into two and when the dimension goes over two, the area becomes contiguous. Because transference beyond the speed of light is impossible any space-time point that energy or information can reach from the origin is limited to the future time-like region. Likewise any space-time point through which energy or information can reach the origin is limited to the past time-like region. Transference in either direction is impossible between the origin and the space-timepoints within the space-like region. In this sense, the light cone represents the barrier due to the limiting speed of light. According to the relativity of simultaneity, the space-like region is the region in which an event can exist at the same time as the origin if a proper system of coordinates is selected. (But these events cannot be observed by an observer at the origin according to the limit of light speed.)
This concept of "space-like region" is a direct result of the theory of relativity. Conventional thinking ignored the existence of an ambiguous region. Therefore space-time was split into the past and future at one cross section plane defining the past, present and future depending on the system of coordinates (vehicle), as the simultaneity was absolute. On the small scale of our daily experience, light velocity was too fast for us to perceive. This is consistent with the concept in those days when the limit value of speed was not yet discovered and infinite speed was believed to be possible. The light cones, determined by the limiting speed of light, were infinitely flattened and the space-like region became nonexistent, if the limit of speed reached to infinitely high. However, in modern times with the advent of space travel and such, we are gradually becoming familiar with the speed of light and the concept of space-like region discovered by the theory of relativity can no longer be ignored.
The geometric representation of the space-time diagram based on the theory of relativity, which Minkowski presented, can be applied to the entire field of mechanics. For example, acceleration can be expressed as the "curvature" of the world line. Momentum and kinetic energy that change the direction of the world line can be regarded as the space and time components of a four-dimensional vector whose length corresponds to static mass in space-time. Mass, the coefficient of inertia, of an object can be interpreted as the difficulty of bending (stiffness) the world line. In this way mechanics can be formulated in the four-dimensional geometry.
Minkowski recognized that the four-dimensionally defined vector is invariant to the transformations of the systems of coordinates (Lorentz transformations). In three dimensional space the distance between two points is expressed by the Pythagorean theorem using the three components x, y and z, but it differs depending on the direction of x, y and z axes. The square root of the sum of the square of each component enables us to obtain their absolute lengths regardless of the directions of the axes based on Pythagorean theorem. By adding a time axis, Minkowski noted that the square root of difference between the sum of the square of each space component and the square of time components was consistent beyond the differences of the axes. This is based on the fact that the formula concerning the spherical surface of light waves is consistent. The consistency of the addition of the square of components in space is a significant characteristic of Euclidean space, which is compatible with the Pythagorean theorem, but the subject of "space-time" is characterized by the consistency of its subtracted differences instead of addition (*1). This characteristic is clearly different from Euclidean space. For instance, the locus of all points equidistant from a certain point constitutes a circle (or a sphere) in Euclidean space, but in Minkowski's space-time diagram, a line representing the same "space-time interval" from a certain point describes a hyperbola. Generally, the distance between one space-time point and another has both time and space intervals. If there is any system of coordinates in which the two points are at the same position (immovable), it is possible to consider a true time interval only on that system. By the same token, if there is any system of coordinates in which the two points can be regarded as simultaneous, it is possible to treat it as a true spatial interval only on that system. However, time and space intervals just represent the cross sections of space-time and cannot be treated separately.
Minkowski argues at the beginning of Space and Time (1908) as follows:
"Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality." (*2)
(*1) If the "consistency in the total addition of the square of the components" is retained as a representational form, it can be mathematically treated as a simple dimensional extension of Euclidean space, and addressing either time or space as an imaginary number becomes necessary.
(*2) Refer to Hermann Minkowski (1908), Raum und Zeit (Published in English as Space and Time by W. Perrett and G.B. Jeffery), p. 103, translated from the original German to Japanese by Kamikawa Tomoyoshi (1969), Tokai University Press.