A PHILOSOPHY OF THE FOUR-DIMENSIONAL SPACE-TIME
The Worldview of Relative Simultaneity (MURAYAMA Akira)
CHAPTER I
Relativity and Four-dimensional spacetime
[The First half] ---- Outlining the Theory of Relativity ----3. The Relativity of Simultaneity, Time Dilation, and the Length Contraction
(2) Time Dilation
These innovative concepts concerning space and time in relation to the invariance of the speed of light introduced not only issues of simultaneity but also novel ideas about the length of space and time.
Einstein's approach was based on the assumption that the unit distance and unit time of the direction in which an object is moving might vary in different systems of coordinates. However, he speculated that the vertical movement of the direction in which an object is going is not affected by relative speed among different systems of coordinates because vertical movement demonstrates a velocity component of zero. It was based on this assumption that Einstein devised his light clock to measure time. He did this by using the unit of the process in which light emitted vertically in the direction that an object is already traveling is then projected onto a mirror at a distance and reflected back. Einstein's light clock was set on each system of coordinates along which the object was moving. The distance between the light source and the mirror was found to be equal for each system of coordinates because of the verticality factor. Time could be obtained by dividing the distance traveled by the speed of light as a constant. This defined unit time. (See Figure 1-3-3.)
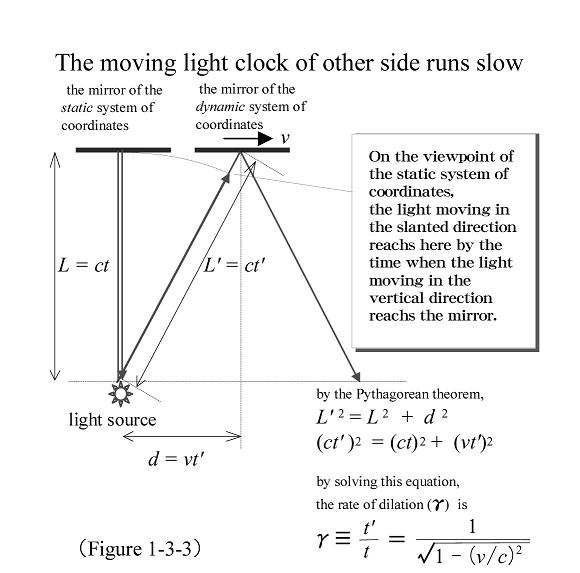
More specifically, the light of a light clock set for A moving toward B appears to travel in an oblique direction for B. The slanted direction covers a longer distance, which means that the light of A moving in the slanted direction takes longer to reach the mirror than the light of B moving in the vertical direction. In other words, the light clock of A runs more slowly. This time dilation can be easily calculated using the Pythagorean theorem. The degree of time dilation γ is expressed as follows:
This formula shows that as v, or the speed between systems of coordinates, gets closer to c, or the speed of light, the degree of time dilation becomes infinitely larger. If the speed between systems of coordinates is negligibly small in comparison with the speed of light, that is, as small as the speed we often experience in our daily lives, the degree of time dilation reflects close proximity to the number one. This means that there are few time dilations. However, if v is 60% (180,000 kilometers per second) of c (the speed of light), then the light clock will give rise to a 1.25-fold time dilation.
These discussions can also be applied when this moving system of coordinates is regarded as a static one, and the static system of coordinates is regarded as a dynamic one that is moving in the opposite direction. In this instance, the light of the second system of coordinates is perceived to be traveling in an oblique direction, therefore suggesting that the light clock of such a system of coordinates runs slowly. However, this does not mean that either of the two systems of coordinates unilaterally runs slowly in absolute implication, but that the light clock is interpreted as running slowly when it is observed from the viewpoint of other side.