A PHILOSOPHY OF THE FOUR-DIMENSIONAL SPACE-TIME
The Worldview of Relative Simultaneity (MURAYAMA Akira)
CHAPTER II The Problems of Continuity and Contradiction
6. The Continuity of Velocity
In the previous section, I noted that the concept of four-dimensional space-time lays the foundations for the existence of movements without infinite dichotomy. This hints at the possibility of movements even if they are not continuous but discrete.
Physical history has found that objects and energy that were conceptually thought to be continuous and compatible with infinite dichotomy have structural minimum units, as the discovery of atoms and the establishment of the quantum theory suggest. In accordance with this reasoning, it is possible to consider that space-time itself is discontinuous and can be quantized. Often the belief is that modern physics aims to demonstrate this.
The theory of relativity is based on the four-dimensional space-time model comprised of three-dimensional space and one-dimensional time, but modern physics seeks to establish a unified theory using a higher dimensional space-time model. When we think about ultra-minute structures under ultra-high density energy (mass), we need to be free from the four-dimensional space-time model. Under usual macro-conditions, however, theoretical models are constructed in such a way that the four-dimensional space-time model is enough. The four dimensionality itself is conditional and universal higher-dimensional space-time models have been established. Theoretical models have been evolving in such a way that usual four dimensionality is just functional enough as structural models under particular conditions (familiar to us). (In the superstring theory, an eleven-dimensional continuous space-time manifold is conceivable.)
The continuity of space-time constitutes the foundations for the theory of relativity. That is, the theory of relativity is positioned in modern physics as a theory justified only within the scope where the continuity of space-time can be assumed. However, it remains to be seen to what extent the continuity of space-time can be assumed. We cannot simply say that the discrete space-time model is valid. The equivalence of inertial systems is one of the factors that makes it difficult to de-emphasize the continuity of space-time.
Modern physics, including the theory of relativity, is based on the idea that all coordinate systems are equal under equal conditions (for example, in an inertial system in a space-time without distortion) and there are neither privileged coordinate systems nor origins in space. Everything is equal in space and our present viewpoints are never special in the entire universe. This thinking has laid the foundations for our frame of reference since the major transformation from the Ptolemaic theory to the Copernican theory and will never be overturned in the future.
Now, based on this thinking, I focus on the discrete space-time model. Figure 2-6-1 is a lattice-shaped discrete space-time model. Suppose that four-dimensional space-time has discrete structure like this from a microscopic perspective. Here are the two inertial coordinate systems A and B with different velocities. Then, problems occur. While four space-time factors pass through A system, only two factors pass through B system. More generally, this lattice-shaped discrete model is not equal in different inertial coordinate systems.
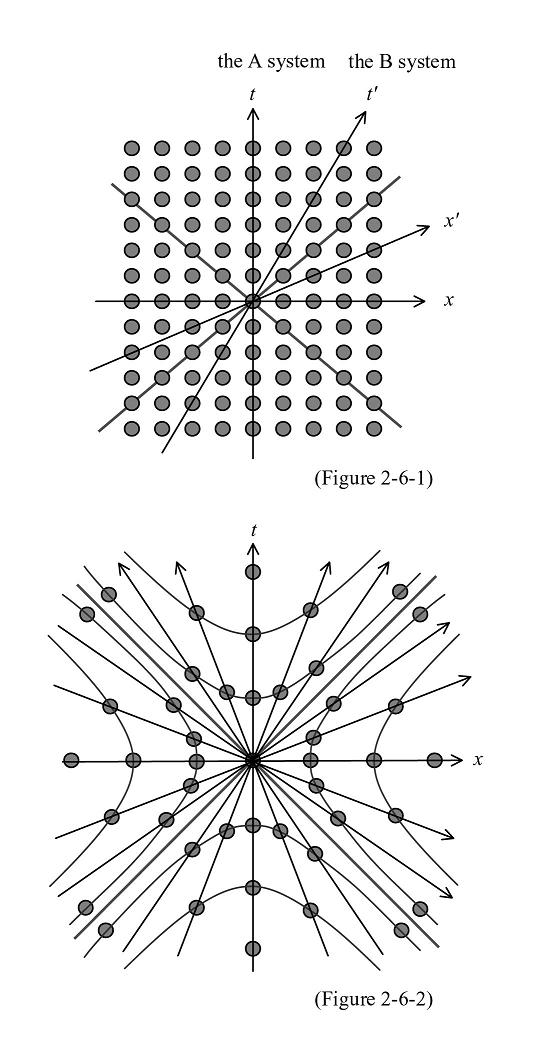
Next, I note Figure 2-6-2, which represents a discrete space-time model based on Minkowski's space-time structure. In Figure 2-6-2, a trajectory drawn by connecting space-time points with an equal distance or time from the origin depicts hyperbolas. Suppose that space-time factors exist along with these hyperbolas. The density of space-time factors is equal in every coordinate system with different velocities. That is, the model has consistent structure in relation to Lorentz transformations (velocity changes) among coordinate systems sharing the origin. However, in this model, the farther space-time factors get from the origin, the less dense they become. To state this in another way, the model cannot retain a consistent relation to coordinate transformations, including translation. This means you have to regard a particular spot at a particular period of time as the absolute center of the universe and this type of discrete space-time model is unacceptable.
In this way, the discrete space-time model cannot be easily established. The continuity of space-time cannot be easily denied. In fact, quantum mechanics does not simply discretize everything. This is because the before-observation state of objects calculated by equations of quantum mechanics is expressed by n-dimensional complex vectors. As complex numbers are combinations of real numbers and imaginary numbers with continuous density, they are continuous numbers. Just as the world is not so simple a continuous thing, it is not so simple a discontinuous thing.
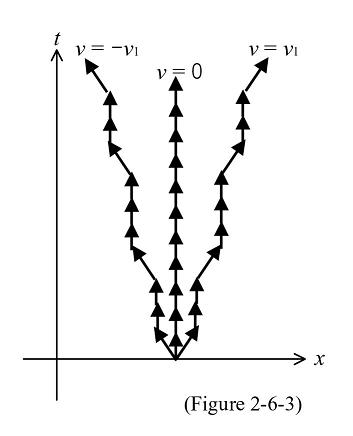
Now, I focus on the continuity of velocity. Figure 2-6-3 illustrates an example of the discontinuous velocity model. Figure 2-6-3 is based on an ultimately minute unit time. Suppose that the speed (the absolute value of velocity) is zero (static) or a particular value (for example, the speed of light) at that unit time. Real specific velocities are realized by adequate combinations of these two kinds of speeds. Suppose that as this time unit is very minute, macroscopically speaking, every velocity is continuously possible. The question is if this model can be demonstrated, being compatible with Minkowski's space-time structure. Unlike Figure 2-6-2, which illustrates a discrete positioning of absolute space-time factors, this model represents a quantization of space-time length (proper time divided by proper distance). It seems unnecessary to pay special attention to the origin, but the question is if the idea of an ultimately minute unit time is possible. The next questions are if it is possible to uniquely retain a part of the world-line with either velocity factor in any coordinate system. Unless a velocity is measured, the question is if this is just an uncertain state of quantum. It is certain that this is not an easy issue. In fact, there have been many studies of the quantization of space-time (manifold) as great challenges and geometry is considered a good candidate for approaching the subject.
What I intend to present in this section is that in the worldview of four-dimensional existence, the continuity of space-time or velocity is likely to stem from the necessity of other perspectives, such as the equivalence of coordinate systems, not from the necessity of making movements possible. Movements are not produced. Movements are a conceptual representation of recognizers and do exist.
Probably, the continuity of velocity reminds you of Zeno's final paradox, the horse paradox. This paradox is that a static object and a moving object whose lengths are the same and that two objects with the same length that are moving in the opposite direction pass each other at the same point of time. In accordance with common sense about relative movements today, this logic is clearly incorrect and is often ignored. With respect to this logic, Hidekichi Nakamura argues in Time Paradox(*2) that the paradoxical characteristics of the logic can be highlighted on the basis of the minimum unit of space and time and that the pitfall of the paradox consists in regarding space and time as measurable combined minimum units. There are probably many ideas about how to evaluate this paradox. I cannot help being astounded by the fact that Zeno left such a discussion that even reminds us of the quantization of space-time.
The question is if continuity is an attribute of existence or just a conceptual thing created upon request in logical thinking. This question is a profound philosophical aporia that has not yet been solved.
(*2) Refer to Hidekichi Nakamura (1980), Time Paradox, Chuko Shinsyo, p. 168.